Abstract
For an n-component system at chemical equilibrium, an assemblage
of n+2 phases is thermodynamically invariant, an assemblage of
n+1 phases is univariant, and an assemblage of n phases is divariant.
On a pressure-temperature diagram, an invariant point could occur
only at some specific temperature and pressure; from this point
there radiate n+2 univariant curves, and from each curve there
emanate n+1 divariant regions. How these univariant curves and
divariant regions are related to one another and how these relations
reflect the relative compositions of the n+2 phases are the subjects
of this paper; the treatment is based largely on the method discovered
by F. A. H. Schreinemakers.
Because each univariant reaction involves n+1 phases, one of
the n+2 phases that occur at the invariant point is missing along
this reaction line. The univariant line, therefore, can be uniquely
identified by the missing phase; by convention this missing phase
label is given in parentheses. This paper demonstrates that for
any given univariant reaction, there exists a corresponding set
of relations among the univariant curves. Thus, if in a ternary
system the heterogeneous reaction
A+B = C+D (phase E missing)
is univariant, then on the p-T diagram the univariant curves
bearing the labels (A) and (B) must occur on one side of the
curve bearing the label (E), whereas the curves bearing the labels
(C) and (D) must occur on the other side of curve (E). Because
each univariant curve contains n+1 phases, any two univariant
curves contain all the n+2 phases, barring compositional degeneracy.
Knowledge of two nondegenerate univariant reactions in the system
thus suffices to determine all the other univariant reactions
and therefore the succession of univariant curves around the
invariant point. When the succession of univariant curves is
known, it is a simple matter to determine next the relative locations
of the divariant assemblages on the p-T (pressure-temperature)
diagram.
The Schreinemakers method can be applied to systems containing
any number of components. For both unary and binary systems,
there is but one corresponding topological arrangement of the
univariant curves; for ternary systems, there are three possible
topological arrangements. The number of possible arrangements
increases rapidly for systems beyond the ternary; however, all
the possibilities can be readily enumerated by means of the "pencil
theorem" of Schreinemakers, which is discussed in detail.
An n-component system is degenerate if one or more of the associated
univariant curves can be described by fewer than n components.
Chemographically, this corresponds to the coincidence of phases
(n=2,3,4, . . . ), colinearity of phases (n=3,4,5, . . . ), coplanarity
of phases (n=4,5,6, . . . ) and so on. The phases participating
in degenerate univariant reactions are the singular phases; those
which do not participate are the indifferent phases. In a degenerate
system, two or more univariant lines assume the same value of
slope at the invariant point. If the indifferent phases are chemographically
on opposite sides of the singular phases, the degenerate curves
coincide stable to stable (so that fewer than n+2 univariant
lines obtain); if the indifferent phases are on the same side
of the singular phases, the degenerate curves coincide stable
to metastable. All the possible cases of degeneracy for binary
and ternary systems are described in this paper.
The method of Schreinemakers is useful in analyzing petrologic
problems. Thus, for a given mineralogical system, if only some
of the n + 2 univariant curves about an invariant point have
been determined experimentally or by calculation from available
thermodynamic data, the application of the method enables one
to compute approximately the remaining curves. Because the chemographic
relations of the phases determine the sequence of univariant
curves about the invariant point, the method is useful in evaluating
the consistency of existing thermochemical data on minerals of
known compositions. Even when no experimental or thermochemical
data are available, knowledge of the chemical compositions of
the phases alone often allows one to calculate and predict the
relative p-T dispositions of mineral assemblages in specified
chemical and mineralogical systems; such knowledge is frequently'helpful
in the study of mineral paragenesis. Examples of the application
of the Schreinemakers method to mineralogical systems are given. |
/Image2433.gif)
FIGURE 3. The Morey-Schreinemakers rule.
The assemblage (n+1, n+2) must be stable in the smaller sector,
for otherwise in the sector marked by the angle 6 this assemblage
must be simultaneously stable and metastable. |
/Image2434.gif)
FIGURE 4. Two enantiomorphic forms of succession of univariant
lines consistent with a given univariant scheme.
The correct choice from the two forms for a given p-T diagram
cannot be determined by the chemographic relations alone. |
/Image2435.gif)
FIGURE 5. The general geometric relations of the three univariant
lines about the triple point in a one-component system. Two enantiomorphic forms are shown; both are consistent
with the relations depicted in figure 6. |
/Image2436.gif)
FIGURE 6. Three isobaric G-T sections (lines) of the G-p-T
surfaces of three polymorphs. A, At p=ps,
the pressure of the triple point, the three lines intersect at
a single point. B, At p = pb, slightly higher (or lower) than ps . C, At
p = pc, slightly lower
(or higher) than pa. In each diagram, the sequence of stable
univariant and divariant assemblages with rising temperature
is given by the lowest set of free-energy lines. Note labels
refer to phases, not phases absent. |
/Image2437.gif)
FIGURE 9. The unique geometric relation of the four univariant
lines about a given invariant (quadruple) point in a binary system. |
/Image2438.gif)
FIGURE 10. Derivation of the geometric relations of a binary
system from that of a unary system. If aa',
bb', and cc' are the three univariant lines of a unary system,
the addition of a fourth line, dd', required by a binary system,
necessarily results its opposite sector having two metastable
extensions. Each of the two flanking sectors has one metastable
extension. |
/Image2439.gif)
FIGURE 11. The p-T diagram in a ternary system where the five
phases form a convex pentagon. A, The
chemographic relations; B, the corresponding p-T diagram.
Notice that the univariant curves follow in numerical sequence
when the phases are labeled in diagonal sequence. |
/Image2440.gif)
FIGURE 12. The p-T diagram in a ternary system where four
of the five phases form a quadrilateral and the fifth phase is
an interior point. See also caption for figure
11. |
/Image2441.gif)
FIGURE 13. The p-T diagram in a ternary system where three
of the five phases form a triangle and the remaining two points
fall inside the triangle. See also caption
for figure 11. |
/Image2442.gif)
FIGURE 14. Derivation of the three types of p-T diagrams for
ternary systems from the unique configuration for a binary system.
Addition of a fifth curve in the sectors labeled
a, 6, or c results in figures 11, 12, or 13, respectively, by
geometric considerations alone. |
/Image2443.gif)
Figure 15. Demonstration of the pencil theorem.
Each stable line labeled PI, Pt, ..., represents a pencil of
stable univariant lines which are not separated from one another
by metastable extensions of other univariant lines. The total
number of pencils is always odd. |
/Image2444.gif)
FIGURE 16. Four possible sets of degenerate relations in a
binary, four-phase system. A heavy dot indicates
that the composition point is shared by two or more phases. |
/Image2445.gif)
FIGURE 17. The p-T diagrams corresponding to the four sets
of degenerate relations of figure 16; A refers to figure 16A
and so forth. Lines with multilabels are degenerate,
that is, each of them represents the coincidence of two univariant
lines. The coincidence may be stable to stable (A and D) or stable
to metastable (B and C), depending on whether the indifferent
phases are on opposite sides or the same side, respectively,
of the singular phases. In all cases, however, three distinct
slope values obtain at the invariant point. |
|
/Image2446.gif)
FIGURE 18. The four possible sets of degenerate relations
among the compositions of five phases in a ternary system (A-D)
effected by the colinearity of three phases and their corresponding
p-T diagram types (E-H). Note that five stable
univariant lines obtain when the indifferent phases lie on the
same side of the singular phases; four stable uni variant lines
obtain when the indifferent phases lie on opposite sides of the
singular phases. In all events, four distinct slope values obtain
at the invariant |
/Image2447.gif)
FIGURE 19. The three possible sets of compositionally degenerate
relations in ternary, five-phase systems effected by a single
compositional coincidence (dimorphism) of two phases (A-C) and
their corresponding p-T diagram types (D-F).
Note that four stable lines obtain when the indifferent phases
are on the same side of the singular phases; three stable lines
obtain when the indifferent phases are on opposite sides of the
singular phases. In all cases, three distinct slopes values obtain
at the invariant point. On the p-T diagrams, only those phases
are labeled whose identities, because of compositional coincidences,
would otherwise be ambiguous. Heavy dots indicate phases with
coincident compositions. |
/Image2448.gif)
FIGURE 20. The three possible sets of compositionally degenerate
relations in ternary, five-phase systems each effected by two
independent sets of three colinear phases (A-C), and their corresponding
p-T diagram types (D-F). Depending on the chemographic
relations of the indifferent and singular phases, five, four,
or three stable univariant lines may obtain, but in all cases
only three distinct slope values obtain at the invariant point. |
/Image2449.gif)
FIGURE 21. The three possible sets of compositionally degenerate
relations in ternary, five-phase systems effected by the colinearity
of three phases and a compositional coincidence of two phases
(A-C), and their corresponding p-T diagram types (D-F). If the two degeneracies are coupled (A, B), three distinct
slope values exist at the invariant point; if the two degeneracies
are not coupled (C), only two distinct slope values exist at
the invariant point. 20A and B correspond to the binary degeneracies
of figures 17C only those phases are labeled whose identities,
because of compositional coincidences, would otherwise be equivocal.
Heavy dots indicate phases having coincident compositions. |
/Image2450.gif)
FIGURE 22. The single possible set of compositionally degenerate
relations in ternary, five-phase systems effected by one compositional
coincidence of three phases, and its corresponding p-T diagram
type. Phases 4 and 5 are absolutely indifferent
phases. On the p-T diagrams, only those phases are labeled whose
identities, because of compositional coincidences, would otherwise
be ambiguous. Heavy dots indicate phases with coincident compositions. |
/Image2451.gif)
FIGURE 23. The single possible set of compositionally degenerate
relations in ternary, five-phase systems effected by two compositional
coincidences of two phases each, and its corresponding p-T diagram
type. Phase 5 is an absolutely indifferent
phase. On the p-T diagram only those phases are labeled whose
identities, because of compositional coincidences, would otherwise
be equivocal. Heavy dots indicate phases with coincident compositions. |
/Image2452.gif)
FIGURE 24. The single possible set of compositionally degenerate
relations in ternary, five-phase systems effected by the colinearity
of four phases, and its corresponding p-T diagram type. The diagram is that of a binary four-phase system,
with an absolutely indifferent fifth phase added. |
/Image2432.gif)
FIGURE 33. Schematic representation of Gibbs free-energy relations
of the phases around an invariant point in a binary four-phase
system. The metastable univariant lines are
extended in full, but are shown as dashed lines. Each G-X plot
is topologically correct for the entire sector as shown; the
Gibbs free-energy values increase upward so that the straight
lines connecting the lowest set of points depict the stable univariant
or divariant assemblages. In each G-X plot, the successively
higher lines connect univariant or divariant assemblages which
are successively more metastable. Where two such lines cross,
for instance between univariant curves (1) and (4), a etastable
fourphase assemblage could form fortuitously; such an assemblage,
however, is not invariant. |
|
|
Zen（1984）による『Construction
of Pressure-Temperature Diagrams for Multicomponent Systems After
the Method of Schreinemakers-A Geometric Approach』から |
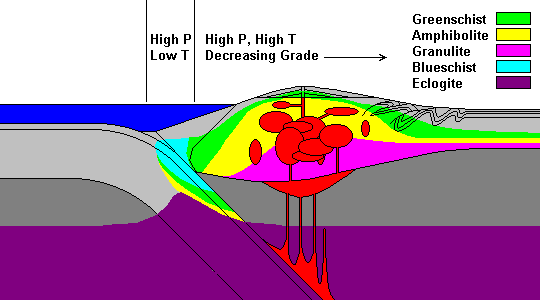
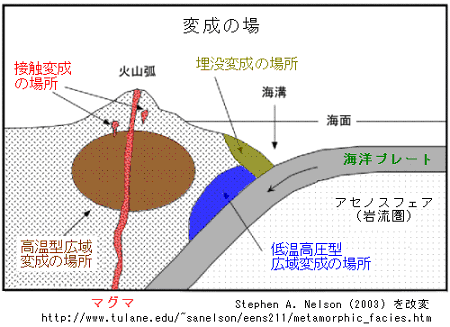
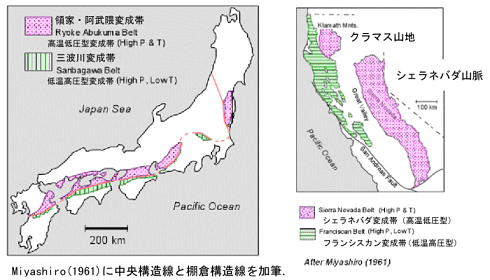
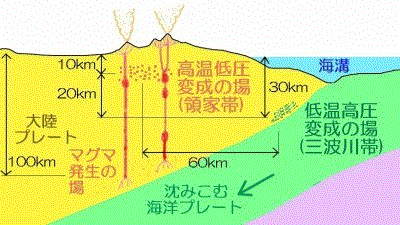
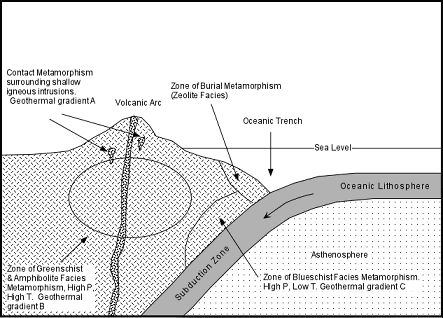
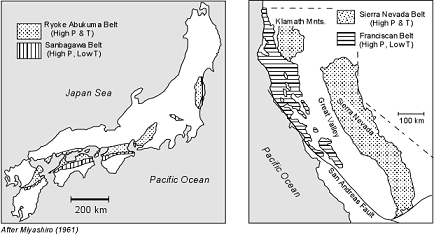
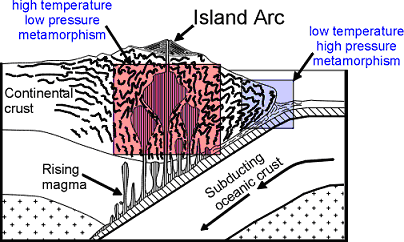
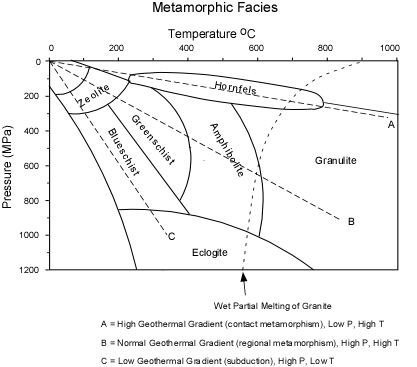
/Image2424.gif)
/Image2410.gif)
/Image2406.gif)
/Image2405.gif)
/Image2409.gif)
/Image2404.gif)
/Image2426.gif)
/Image2427.gif)
/Image2428.gif)
/Image2431.gif)
/Image2425.gif)
/Image750.gif)
/Image751.gif)
/Image752.gif)
/Image749.gif)
/Image745.gif)
/Image747.gif)
/Image746.gif)
/Image748.gif)
