鉱物資源を考える（１）／（２）／（３）／（４）／（５）／文献｜戻る

『鉱物資源を考える』

『�X．　どのくらいあるか
　１．　地質学的な量と鉱業的な量
　（１）　鉱床の量と粗鉱の量　　　探査の結果地質学的に見つけられた鉱床全体の中で、実際に採掘の直接対象となる部分は、種々の自然的・技術的・経済的その他の理由で、一般的にはその全部ではない。例えば、一つの鉱体内での目的鉱物・目的成分の品位分布は極めて不規則なのが普通なので、地質学的には明らかに鉱床の一部でありながら、局部的な低品位のために採掘の直接対象となり得ない部分が、どの鉱床にも何がしか必らずある。あるいは、その規模が部分的に小さすぎるために採掘対象から外される場合もある。一方それらとは逆に、鉱床の形・大きさ・母岩の性質などに関係して、鉱石採掘の際母岩の一部の混る事が技術的・経済的に避け得ない場合もしばしば起る。この場合の母岩の破片はズリと呼ばれる。実際に採掘される粗鉱中でのズリの占める割合い（ズリ混入率）は、日本での実例を挙げると、計画上でのズリ量／粗鉱量の重量比で金属鉱床の場合には10-40％、非金属鉱床の場合には1-20％程度と言われている（資源エネルギー庁、1982）。つまり、探査の結果発見された自然物としての鉱床に対して、種々の条件を入れて採鉱計画を立て、実際に掘るべき場所（鉱画）を決めるのに当っては、ある場合には鉱床の一部を欠き、またある場合には母岩の一部の加わる事が、ごく普通に起る。なお採鉱工程での実収率は、上の場合の外に、計画上の可採粗鉱量と実際に採掘された粗鉱量との重量比で示される場合もある。
　上のような事情で、探査の結果確かめられた鉱床の形・大きさ・鉱床内の品位分布・鉱石の比重などについての諸測定資料を基に計算される自然物としての鉱床の存在量、すなわち鉱床の質量（これを鉱床量とよぶ。場合によってはその中での目的鉱物・目的成分の総含有量で表わされる事も多い）と、採鉱計画上定められた鉱画から実際に採掘を予定される部分の質量（可採粗鉱量。これもその中での目的鉱物・目的成分の総含有量で示される事もある）とは、同じ一つの特定鉱床に対して一般には一致しない。前者は自然に与えられた量（地質学的な量）だが、後者は自然条件と共に技術的・経済的条件なども加わって、いわば人為的に決められる量（鉱業的な量）である。また同じ理由で、鉱床全体の平均品位あるいは鉱床中での目的鉱物・目的成分の総含有量は、自然に決っている地質学的な量だが、採掘される粗鉱の平均品位あるいはその中での目的鉱物・目的成分の総含有量は、ズリ混入率がどのくらいかあるいは採掘限界品位をどのように定めるかなどの諸条件に従って、いろいろに変わり得る鉱業的な量である。
　これにより一般的に言いかえると、鉱床量などの地質学的な量は、一つの特定鉱床に対しては自然に決っている特定の量だが、それに対する可採粗鉱量などの鉱業的な量は、前者とは違ってその時々に考えられる技術的・経済的諸条件にも左右されて、同じ一つの特定鉱床に対しても増したり減ったりし得る可変量である。これらの関係を表�X-1にまとめ、またそれを模式的に図�X-1に示す。

表�X-1　地質学と鉱業との間での概念・量の違い（１）
地質学上の概念・量	鉱業上の概念・量
鉱床（その定義の中に鉱業上の概念を入れない）	有用鉱床（economic mineral deposits）*1 経済限界下鉱床（subeconomic mineral deposits）
鉱床量（geologic bodyとしての質量）	採鉱計画−鉱画・ズリ混入率・採掘限界品位･粗鉱平均品位 埋蔵鉱量（reserve）*2 可採粗鉱量（minable ore reserve）
鉱床中での品位分布 鉱床での平均品位	採掘限界品位（cut-off grade） 粗鉱平均品位（mean ore grade）
鉱床中の目的鉱物・目的成分の含有量 同品位分布	粗鉱中の目的鉱物・目的成分の含有量 同品位別分布
	総鉱物資源量 （total mineral resources）	埋蔵鉱量（reserve） 准埋蔵鉱量（marginal reserve） 経済限界下鉱物資源量（subeconomic resources）
		潜在鉱物資源量（undiscovered resources）
大陸地殻上部での総鉱床量 海洋地殻上での総鉱床量	大陸地殻上部での総鉱物資源量 海洋地殻上での総鉱物資源量
*1　鉱物資源の対象としては、鉱種によっては普通の岩石の一部も含まれる。*2　ここでの埋蔵鉱量（reserve）の定義は、後に示す２．鉱物資源およびその量の区分を参照。

図�X-1　地質学と鉱業との間での概念・量の違い（2）。（別ウィンドウに拡大）


図�X-2　ある斑岩銅鉱床での品位別鉱石量と同鉱石中含銅量の分布。（別ウィンドウに拡大）

　上の関係を一つの具体例について考えてみよう。図�X-2は、ある実在の斑岩銅鉱床を探査して確かめられたその品位別鉱石量（図中の曲線O-1、この例では鉱石の銅品位0.05％きざみの鉱石量を打点してある）および品位別鉱石中含銅量（曲線M-1、同前）と、累積鉱石量（曲線O-2、高品位側から順次加えてある）および累積鉱石中含銅量（曲線M-2、同前）とを、それぞれの曲線で示したものである。今仮にこの鉱床に対する採鉱計画として採掘限界品位を銅0.5％と決め、採掘実収率を100％、ズリ混入率を0％とそれぞれ仮定すれば、これに対応して採掘される鉱石の全量はおよそ1.5億トン（図中の曲線O-1に対してA-C線より右側の部分の面積に相当）、その平均品位は銅0.66％、同じく採掘鉱石中の含銅量は約98万トン（曲線M-1に対してA-B線より右側の部分の面積に相当）と見積られる。
　これに対して、仮に採掘限界品位を銅0.3％にまで下げ得るとすると、採掘鉱石量はおよそ2.8億トン、その平均品位は銅0.53％、採掘鉱石中の含銅量は約150万トンとなる。この場合には、採掘限界品位を銅0.5％から0.3％に下げる事によって、採掘鉱石量は前の場合のおよそ1.9倍にまで上がるが、採掘鉱石中の含銅量は1.5倍にまでしか上らない。採掘限界品位をどのくらいにするかは、鉱床の持つ自然条件のほかに、その時々の技術的・経済的その他の諸条件にも大きく左右されて、一つの鉱床に対しても決して一定不変のものではない。

図�X-3　足尾鉱山横間歩ヒ（金偏に通）で実際に採掘された部分（黒色部）を示す図。
（Nakamura,T., 1970）（別ウィンドウに拡大）

　もう一つ別の例を挙げておこう。栃木県足尾鉱山は17世紀初頭以来稼行の記録の残っている日本でも有数の大規模な銅･錫などの多金属鉱脈型鉱床より成る鉱山である。ここの鉱床は極めて多数の大小の鉱脈より成る一つの鉱脈群で、その中の最も規模の大きい横間歩ヒは、水平（走向）方向におよそ2キロメートル、垂直（傾斜）方向におよそ1キロメートルほどの範囲で開発･稼行された。図�X-3は、この横間歩ヒに沿った縦断面図（この場合鉱脈の傾斜がごく急なのでおよそのところこの紙面が鉱脈そのものと考えてよい）である。ここに黒く塗り潰された部分は実際に採掘されたところ、白く残っている部分は、そこでの鉱脈品位が低すぎるとか脈幅が狭すぎるとか種々の理由で、採掘の対象とはなり得なかったところを、それぞれ示している。この図を見れば、地質学的には1本の鉱脈としてその連続性がよく確かめられておりながら、種々の理由で掘り残されてしまった部分が随分たくさんある事が良く判るだろう。
　鉱物資源の問題を数量的に取扱う場合には、いろいろな数値が利用される。この場合、上の諸例で良く判るように、それが地質学的な量なのかあるいは鉱業的な量なのか、また鉱床量･粗鉱量であれば鉱石の量かあるいはその中の目的鉱物・目的成分の含有量なのかなど、それぞれの数値の持つ具体的内容を十分に正しく理解して利用する事が是非必要である。またこれら数値の単位も、場合々々により種々のものが習慣的に使われて来ており、各種資料の比較検討に当っては、この点にも十分な注意が必要となる。ここでは便宜上、各種の量はすべてメートル制で表わし、可能な限り元素量で示すようにしてある。従って、原資料の数値は必要に応じてすべてこれに換算してある。
　鉱業的な量は、その源となる鉱床についての地質学的な量、すなわち鉱床量･その中での目的鉱物・目的成分の品位分布・その総含有量あるいは規模などの各種基礎資料が、十分に精しくかつ具体的に備えられてさえいれば、どのような技術的・経済的条件に応じても必要な数値を計算して計画を立てる事が出来るはずのものである。しかし、その逆は成り立たない。何よりもまず詳細かつ正確な地質学的諸性質とそれに関する数値資料とを得る事が、その後の鉱業諸工程を計画・立案しさらに実施するための一番の基礎となる。
　（２）　鉱床量･粗鉱量などの見積もりの確からしさ　

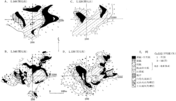
図�X-4　小坂鉱山内の岱西鉱床の坑内地質図。
（加茂野・石川、1965）。（別ウィンドウに拡大）

　図�X-4のAとBとをよく見くらべて欲しい。これらは共に、秋田県小坂鉱山黒鉱鉱床の一つである内の岱西鉱床の140メートル水準地並での坑内地質図である。これらは、場所としてはまったく同じ所のものなのだが、作った時期が違っている。Aは、地表からの数少ない試錐探査だけによって地下深くに新らしく発見された鉱床に対して、そのどくあらましの様子が判った時期に、試錐コアについての調査・測定結果を基本資料とし、それに黒鉱鉱床につきそれまでに得られていた一般的な知識･経験・理論を加えて、いわばごく僅かの具体的資料に多くの推論を加えて作ったものである。これに対してBは、その後この地域にさらに多くの試錐探査を行いまた何本かの坑道をも掘って、試錐コアについての資料と共に、坑道面（連続露出面）で実際に鉱床や母岩について直接観察を行い、かつそこからの採集標本についてのより精しい測定結果をも併せて、全面的に作りなおした坑内地質図である。これらを一見して、開坑前のもの(A)は図の模様（各種の岩石や鉱石の分布状態およびそれらの間の地質学的関係を示す）が随分簡単だが、開坑後のもの(B)はそれに比較してずっと複雑になっている（前述の事柄がより詳しく記載されている。つまり地質図としての精度がより高くなっている）ことがよく判るだろう。また同図のCとDとは、同じ鉱床の120メートル水準地並（前記のA・Bより垂直的に20メートル上方）での開坑前(C)と開坑後(D)との坑内地質図である。これらにも先に述べたのと同じ事情がよく示されている。ところで、BとDとに示されている坑内地質図を比較すれば、同じ一つの鉱床内でも水平・垂直両方向とも、僅かの距離をへだてただけで、鉱床の性質が部分により随分変わっている事がよく判っていただけるだろう。
　このような著るしい違いの生じた原因の第1は、なによりもまず、黒鉱鉱床を作る各種鉱石やそれに伴う各種岩石の分布状態や諸性質の変化が、垂直的にも水平的にも、一般の人が想像する以上に細かく変っている事にある。この場合で言えば、例えば水平方向に100メートルあるいは50メートルも離れれば、それぞれの地点に分布する岩石や鉱石の種類が違ってしまう事は、ごく普通に観察される現象である。はなはだしい場合には、1メートルまたは10センチメートル離れただけでも変わる事も稀らしくはない。これをより一般的に言い表わせば、同じ一つの種類の岩石や鉱石から成る一つの岩体または鉱体の空間的拡がりの規模（形や大きさ）は、しばしばそれほど大きくはないという事である。
　このような事情で、ここでの正確な地質図を作ろうとすると、私たちの観察または試料採集が100メートルおき50メートルおきの程度ではまったく不十分で、少なくともメートル単位、出来得る限り連続した露出面での十分な直接観察や試料採集が行われなければ、精度の高い地質図は作れないという事になる。実際に、図�X-4のA・CとB・Dとの間には、使われた観察結果や試料数に関して量と共に精しさの点でも大きな差があった。もっとも、これほどまでに細かな観察や試料採集を行わなくともその性質を十分正しく知り得るような、より均質かつ連続性が良くて規模の大きな岩体や鉱体もまたたくさん実在している。要は、それぞれの場合ごとに、対象となる地層･岩体・鉱体の持つ諸性質の変化の規模に良く合った精しさでの正確な調査・試料採集・測定が必要という事である。
　この小坂鉱山内の岱西鉱床の鉱床量と平均品位とについて、開坑前と開坑後との2時期に別々に見積られた値の間には、ほぼ10％の差が出ている（加茂野・石川、1965）。この差を大きいと思う人もいるかも知れないが、先に述べた黒鉱鉱床の地質学的性質の特徴から考えると、これはむしろ良く合いすぎているとすら考えられる値である。この開坑後の見積り値ですら、その後の開発･採鉱に際して得られたより詳しい資料に基づいて再検討された値とはある程度違っている。この例のように、一つの鉱床に対して正しい鉱床量･平均品位などの値やさらにそれらを基にして作られる可採粗鉱量や粗鉱平均品位などの正しい数値資料を得る事は、一般に極めてむずかしい作業と言って良い。従って、対象となる鉱床の出来方や一般的諸性質の違い（これに関する知識･理論は地質学1分科で鉱床を直接の研究対象とする鉱床学の発展によって得られる）と、それぞれの場合の探査方法の違いやその精しさの程度などの組み合せ方によって、得られる結果の確からしさの程度は大きく変って来る。しかもその大きさは、一般的に言ってそれほど良いものではないと言わざるを得ない。
　例えば、探査がある程度以上に進んだ鉱床に対して見積られる鉱床量または可採粗鉱量などの値は、通常探査の精しさの程度に応じて確定・推定･予想の3段階に分けて記録されるのが、全世界を通じて行われている方法である。それぞれの区分に対して確からしさの程度を数値で具体的に示す事は、一般には仲々むずかしい。しかし例えば、アメリカ合州国鉱山局と同地質調査所とによる鉱物資源量区分（USGS、1976）によると、この場合誤差の値は確定埋蔵鉱量に対して+/-20％以内とされており、これとほぼ同じ内容を持つと考えられる鉱量に関してソ連邦では10％前後とされている（岸本文男、1976）。推定･予想の区分のものともなれば、それらの見積り値の確からしさは、当然の事ながらより低くなる。

　２．鉱物資源およびその量の区分
　先に述べたように、鉱物資源の量に関するこれまでの区分は、何らかの地質学的な具体的資料の得られた、すなわち低どの差こそあれ地質学的にその存在・性質などがすでに知られた鉱床（既知鉱床）、しかもそのほとんどが有用鉱床に対して、その存在量（鉱床量）または可採粗鉱量あるいはその中での目的鉱物・目的成分含有量などを、確からしさの程度によって確定・推定･予想の3段階に区分するものだった。
　しかし、近年では鉱物資源に関しても相当長い将来にわたっての予測・評価という事が重要な問題となって来たのに対応して、単にすでに存在の知られた有用鉱床に対してのみならず、すでに見つけてはあるが低品位その他の種々の理由で、少なくともここ当分の間はまったく利用し難いと考えられるような鉱床に対しても、同じ区分システムの中に組み入れてその存在量を考えに入れる必要が大きくなって来た。さらに鉱業的には未開発の地域についても、そこの地質環境に関する基礎知識および鉱床の出来方に関する一般的な知識･理論が進んで来ると、それら両者の組み合せによって未知の地域にどんな鉱種・型式の鉱床がありそうか、また場合によってはどのくらいありそうか、などの推定も理論的にある程度可能となって来た。もちろん、それらの存在量についての見積りが出来たとしても、その値は既知鉱床に対するものより確からしさの程度がずっと低いのは止むを得ない。
　上の事情を反映して、最近各国の政府機関や研究機関などから鉱物資源およびその量の新らしい区分や命名法がいくつか発表されている（例えば、カナダ−Zwartendyke,J.(ed.), 1975；アメリカ合州国−USGS, 1976, USBM & USGS, 1980；国連−Schanz,J.J.,Jr., 1980など）。これらはいずれも、基本的な考え方として一方ではその地質学的な確からしさ、他方ではその経済的利用可能性の大きさとの2本の柱を中心に行われている。ここではその1例として、アメリカ合州国鉱山局と同地質調査所とが共同して決めた方法（USBM & USGS, 1980；立見辰雄、1983）を紹介しておこう。表�X-2はその結果をまとめて示したものである。この方法では、横軸に見積り値の地質学的な確からしさの程度（右から左に行くほど高い）、縦軸には経済的利用可能性の程度（下から上に行くほど高い）とを、それぞれ採ってある。前者は既知鉱床−既知鉱物資源量と潜在（未発見）鉱床−潜在鉱物資源量とにまず2大別し、それらは表のようにさらに細分されている。後者は有用鉱床−埋蔵鉱量･准埋蔵鉱量と経済限界下鉱床−経済限界下鉱物資源量とに分けられると理解して良いだろう。これらを量に関して別なまとめ方をすれば表�X-3のようになる。

表�X-2　鉱物資源量の区分（１）（USBM & USGS, 1980）
累積 生産量	既知鉱物資源量			潜在鉱物資源量
	確認		予測	確からしさの程度
	精測	概測		仮定	純理的
経済的	埋蔵鉱量		予測 埋蔵鉱量
准経済的	准埋蔵鉱量		予測 准埋蔵鉱量
経済限界下	確認経済限界下 鉱物資源量		予測 経済限界下 鉱物資源量
その他の産出	非在来型および極低品位鉱床の量

表�X-3　鉱物資源量の区分（２）
総鉱物 資源量	既知 鉱物 資源量	１．埋蔵鉱量（reserve）* 　a.　すでに見つけてあり、かつ現在の諸条件の下で経済的に利用可能な鉱床〔有用鉱床〕に関する量−埋蔵鉱量 　b.　上に準ずるが、特に経済性の点で限界すれすれのもの−准埋蔵鉱量
		２．鉱物資源量（resources） 　a.　すでに見つけてあるが、低品位その他の理由で、現在では利用し得ない鉱床に関する量−既知経済限界下鉱物資源量
	潜在−	b.　未知の地域にその存在が地質学的に期待される鉱床に関する量−潜在鉱物資源量
*　ここでは確認（精測＋概測）および予測の両者を含む。ただし、埋蔵鉱量と記した場合、しばしば前者のみを指す事がある。また、日本工業規格JIS-M1001による“埋蔵鉱量”の定義は、その文面からすれば本来の鉱床量と一致するようにとれるが、実際の各企業での計算の場合には、それぞれの鉱床に対して具体的に決めたある鉱石品位以上の部分についてのみを計算している場合が多いように思われる。

　ここで言う埋蔵鉱量の定義は次のようになっている−既知鉱物資源量の中で、現在の採掘および生産の操業に関係した、はっきり限定された物理的・化学的最低規準を満す部分の中で、考える時点で経済的に採掘または採掘され得る部分（USBM & USGS, 1980）。この内容によれば、ここでの埋蔵鉱量は、よく使われるminable ore reserveとかrecoverable ore reserveあるいは日本工業規格JIS-M1001による可採粗鉱量などとほぼ同義のように思われるが、必らずしもはっきりしているわけではない。経済限界下鉱物資源量の場合には、その実状から判断してその多くあるいはほとんどは地質学的な鉱床量で示されていると考えて良いだろう。ある機関では、個々の鉱床についてではなく、国または全世界のような大きな単元で鉱物資源の量を考える場合には、最初は鉱床量（in situ resources）またはその中の目的鉱物・目的成分の含有量で表わし、区分が細かくなるのにつれて鉱業的な量として、最終的には採鉱実収率の事まで考えに入れて表わすという方法を提案している（Schanz,J.J.,Jr., 1980）。
　埋蔵鉱量にしろ他の鉱物資源量にしろ実際に発表されている値は、そのごく一部で採鉱実収率（この場合は、計画された可採粗鉱量と実際に採掘された粗鉱量の比）が考えに入れられているだけで、選鉱・製錬工程での実収率まで考えに入れて計算されている例はまず無い。従って、これらの発表された数値を使って実際に鉱物資源の将来を量的に考える場合には、次の事にも十分注意を払う必要がある。例を銅にとって考えてみよう。銅の埋蔵鉱量については、銅鉱石中の含銅量として1980年度には4.94億トンあるとの見積りが発表されている例がある（USBM, 1981）。この銅分は、将来銅鉱石として採掘され、さらに選鉱・製錬の諸工程を経て、最終的には電気銅として諸工業の原材料となる。すでに述べたように鉱業の諸工程での実収率の事を考えに入れると、埋蔵鉱量として与えられた銅量のうち将来電気銅として実際に利用され得る分は、条件の良い場合でその70％程度、悪ければ50-60％前後と考えられる。前に挙げた埋蔵鉱量の数値を基にすれば、この量は良くて3.5億トン程度、悪ければ3.0-2.5億トン前後にまで下る。銅鉱物資源の将来の需要または供給の問題を考える場合に、これを銅鉱石中の含銅量で考えるのか、あるいは工業原料としての電気銅の量で考えるのかによって、上に与えられた埋蔵鉱量としての4.94億トン（1980年度）という数値の具体的意味も変わって来る事になる。また、特定鉱種の鉱物資源の耐用年数（寿命）を考える場合にも、同様の点に十分注意する必要がある。
　化石エネルギー資源の場合には、先に述べたのとは違った方法で定義された諸量が使われる事が多い。それは、例えば石油鉱床の場合で言えば、これと他の鉱物資源との間の自然科学的な諸性質の違いやその開発・利用に当っての技術的方法の違いなどによるためで、それらの特徴が諸量の定義の中に良く表われている。

　３．　既採掘量と既知鉱物資源量の見積り
　（１）　既採掘量　　　これまでにすでにどのくらいの量の鉱石を掘ってしまったか（既採掘量）については、過去の記録を丹念に拾い集めて集計すれば結果が得られる。しかし、近年の記録はともかくとして、何100年も何1000年も前の古い事となると、その正確な資料を残りなく得る事は実際上出来ない。この分については勢い少数の資料からの推計に頼る事になるので、それだけ確からしさに劣るのも止むを得ない。しかしすでに述べたように、各種鉱石の年生産量は産業革命以降急激に増して来ており、従ってこれまでの既採掘量の大部分はこの僅か200年ほどの短期間の分によって占められている。この間の記録は比較的よく残されているので、それら全てを集計して得られる既採掘量に関する最終結果は、少なくとも2-3桁ぐらいまでに数値だったら、大きな誤りを犯す事はほぼ無いと考えても良いだろう。
　ここには、資料の得られた銅･鉛･亜鉛・ニッケル・金･ウランの6鉱種についての1979年度末までの全世界既採掘量を表�X-4として掲げる。なおこの表には、1980年度でのそれらの埋蔵鉱量の値もつけ加えてある。例えば銅については、鉱石中含銅量にして1979年度末までにおよそ2.3億トンを掘り、1980年度までに全世界ですでに見つけてしまった銅の有用鉱床の鉱石中含銅量は前の値に埋蔵鉱量の値を足しておよそ7.3億トンという事になる。この値をここでは一応既発見量と呼ぶ事にしよう。もちろん、本来の意味での既発見量は、さらに既知経済限界下の鉱物資源量（海洋地殻表層部の分も含む）をも加えた値だから、この数値よりももっと大きい筈である。

表�X-4　銅･鉛･亜鉛･ニッケル･金･ウラン鉱物資源の既採掘量と既発見量
	鉱種	単位 (t)	既採掘量（鉱石中含金属量）					埋蔵鉱量*3 (1980 含金属量)	既発見量(B)*4 (〜1980 含金属量)	A/B (1980 ％)
			期間�T*1	量	期間�U*2	量	計（A） (〜1979)
世 界	Cu	×106	〜1972	180	1973-79	51.8	232	494	726	32.0
	Pb	×106	〜1965	141	1966-79	39.6	181	127	308	58.8
	Zn	×106	〜1965	155	1966-79	76.8	232	162	394	58.9
	Ni	×106	〜1979	11.6*5			11.6	73.1	84.7	13.7
	Au	×103	〜1975	85*6	1976-79	4.9	90	32.3	122	73.8
	U*7	×103	〜1974	429	1975-79	142	571	79　2.59×106	79　3.16×106	79　18.1
日 本	Cu	×106	〜1959	5.0*8	1960-79	1.9*9	6.9	0.96*10	7.9	87.3
	Pb	×106	〜1959	0.62	1960-79	1.1	1.7	0.76	2.5	68.0
	Zn	×106	〜1959	7.57	1960-79	4.6	12.2	4.21	16.4	74.4
	Au	×103	〜1959	0.50	1960-79	0.13	0.63	0.04	0.67	94.0
*1　Pelissonnier,H.(1972,75)、矢島淳吉(1976)。*2　1966-68：Metalgesel schaft, 1966-68；1969-79：USBM(1981)、USBM Bull. 671。*3　USBM(1981)。*4　既採掘量＋埋蔵鉱量。*5　Riss,J.R. & Travis,G.A.(1981)。*6　Boyle,R.W.(1979)。*7　動力炉核燃料事業団(1980)。ソ連圏を含まない。*8　関根良弘(1962)。*9　資源エネルギー庁(1980)　資源統計年報1979．*10　同左(1982)　鉱業便覧昭和56年度版。

　表�X-4に与えられている資料を基に計算すると、ここに掲げた鉱種に関しては、これまでに見つけた全量（既発見量）のうちすでに掘ってしまった分の割合には、
　銅−32.0％、鉛−58.8％、亜鉛−58.9％、金−73.8％、ニッケル−13.7％、ウラン−18.1％
となっている。人類が古くから利用して来た鉱種（銅・鉛・亜鉛・金）とごく近年になってから利用し始めた鉱種（ニッケル・ウラン）とでは、この値に美事な差が出ている。これらの値を具体的に知って、もうこんなに使ってしまったのかと思うか、あるいはまだこんなに残っていると思うかは、人によってそれぞれに異るだろう。しかし、最近での鉱石年生産量とその生長率との著るしい大きさを併せ考えると、いずれにしても決して安心の出来る値ではないと考えたい。
　なお、表�X-4には日本の場合についても銅･鉛･亜鉛・金の4鉱種について同様の資料を示しておいた。これを世界全体についてのものと比較すれば、日本の場合の情況が極めて悪い事がはっきり理解出来るだろう。なおここで一つ朗報を記しておこう。ごく最近に鹿児島県に発見された菱刈金鉱山の場合には、その鉱床量は鉱石中含金量にして120トンという莫大な値で、日本での既採掘量のほぼ20％にも達すると言われる。この値を加えて再計算すれば、既採掘量／既発見量比の値は約10％ほど表中の値より下がる。
　（２）　既知鉱物資源量　　　これには、総鉱物資源量のうち埋蔵鉱量･准埋蔵鉱量と既知経済限界下鉱物資源量とが含まれる。その精しさ・確からしさにはいろいろな程度の差はあるが、いずれも十分なあるいは何がしかの地質学的調査や試料採集などの探査活動がすでに行われていて、計算の基礎となる各種測定資料のある個々の鉱床の鉱床量あるいは可採粗鉱量の値をすべて足し合せて得る量である。実際には、この種の基礎資料のすべてが公表ないし入手可能というわけでもないし、また既知鉱床と言っても探査の進み具合いは個々の鉱床によって随分違うので、その最終的な累積値の確からしさは決して良いものではあり得ない。
　a)　大陸地殻上部　　　各種鉱物資源の見積り値は、多くの調査機関あるいは個人研究者によってたくさん発表されている。実状は、ある一つの特定鉱種を選んで互いに比較検討してみれば、大き目のものから小さ目のものまでいろいろあって、その何れがより正確なのかを判定するのは誠にむずかしい。いずれにせよ、結果としての数値だけではなくて、それが導き出されるまでの道すじやそこで使われた基礎資料なども十分吟味されなければならず、これは決して容易な事ではない。ここにはその1例として、アメリカ合州国鉱山局の発表したものの中からいくつかの代表的鉱種を抜き出して、表�X-5として示す。これは既知鉱物資源量についての表なのだが、統計の都合上一部の鉱種については潜在鉱物資源量の入っているものもある事を注意しておく。この表に示されている各鉱種についての値が鉱物資源の将来に対してどんな意味を持っているのかについては、後の章で議論する事にしよう。

表�X-5　既知鉱物資源量（鉱石中含有目的成分量、1980）
鉱種	単位 （トン）	既採掘量 （〜1979）	既知鉱物資源量
			大陸地殻*1			海洋地殻表層部*2
			埋蔵鉱量	その他	合計	予測埋蔵鉱量	鉱物資源量
Fe*3	×109		93.4	104	197
Mn	×109		1.36	1.45	2.81	6	16.3
Cr*4	×109		3.36	29.3	32.7
Ni	×106	11.6	60.0	168	228	290	760
Co	×106		2.40	3.04	5.44	60
Mo	×106		9.48	11.4	20.9
Ti	×106		273	424	697
Cu	×109	0.232	0.494	1.13*5	1.62*5	0.240	0.689
Pb	×106	181	127*6	161*7	288
Zn	×106	232	162*6	163*7	325
Sn	×106		10.0	27.0	37.0
Sb	×106		4.36*6	0.81*7	5.17
Au	×103	90	32.3	29.0	61.3
Ag	×103		253	517	770
Pt族	×103		36.7	63.3	100
Al*8	×109		4.72	3.31*5	8.03*5
P*4	×109		34.5	95	130
K	×109		7.6	112	120
S	×109		1.77	4.67	6.44
工業用ダイアモンド*4	×100				136
石綿*4	×106		142	105	247
石墨*4	×106		27.1	127	154
カイアナイト類*4	×106		136	317	453
カオリン*4	×109				11.1
耐火粘土*4	×109				68.9
滑石類*4	×109		0.30	1.2	1.5
*1：USBM(1981) Mineral Facts and Problems、*2：Aacher,A.A.(1979)、*3：回収可能量、*4：鉱石量、*5：潜在鉱物資源量を含む、*6：確認埋蔵鉱量のみ、*7：予測埋蔵鉱量＋一部の既知経済限界下および潜在鉱物資源量、*8：ボーキサイト鉱床のみ

表�X-6　世界自由経済圏（含ユーゴスラビア）の銅の埋蔵鉱量（×106t Cu；1979）
	A (251)	B (49)	C (516)	計 (816)	％
ヨーロッパ　鉱石量 　　　　　　　　品位	4.84 0.67	3.27 0.46	0.82 0.54	8.93 0.56	2.01
北アメリカ	56.41 0.70	9.73 0.77	86.75 0.56	152.89 0.62	34.43
ラテンアメリカ	80.52 1.00	27.70 0.69	47.35 0.71	155.57 0.83	35.03
アフリカ	52.31 2.54	0.99 1.37	12.16 1.75	65.46 2.38	14.74
アジア	18.90 0.66	2.82 0.66	14.93 0.53	36.65 0.60	8.25
オセアニア	8.27 0.90	0.30 1.40	16.02 0.61	24.59 0.69	5.54
合計	221.25 0.98	44.81 0.69	178.03 0.62	444.09 0.77
A−現在稼行中の鉱山、B−開発年度のほぼ確定している鉱床および一時休山していたが近い将来再開が確実視されている鉱山、C−探鉱中または探鉱は終了したが未開発の鉱床（鈴木昌也ほか、1980）

　なお比較のために、銅に関して日本の民間会社が別途に資料を集めて推計した結果を表�X-6として掲げる。ここに与えられている世界の銅の埋蔵鉱量（鉱石中含銅量、1979年度）の値4.44億トンは、表�X-5中のそれ4.94億トン（1980年度）と10％ほどの差しかない。ただし前者にはソ連圏の大部分が含まれていない。なお表�X-6には各地域別の値も載せられている。存在比の多い北アメリカ（34.4％）やラテン・アメリカ（35.0％）などの諸地域には、銅鉱床の中では規模の大きい型式である斑岩銅鉱床や塊状硫化物銅鉱床がたくさん見つかっていて、この比の大きくなる原因となっている。
　b)　海洋地殻表層部　　　海洋地殻表層部に発見されている鉱物資源としては、深海底に存在するマンガン団塊鉱床中のニッケル・コバルト･銅などが注目を浴び出してからもう随分時間が経った。この種の鉱床の鉱物資源量としては1960年代前半にMero（1965）が巨大な値を発表して以来多くの調査研究結果が報告されているが、この値は調査が進むのにつれて次第に小さくなって来ているようである。ここには、比較的最近に発表された資料として表�X-7を挙げておこう。この資料はMeroらのものとは違って、鉱業的諸条件を相当細かく決めて算出されたものである。マンガン団塊鉱床の調査・研究は最近でも活発に行われているので、ここに掲げた資料も今後改訂される余地は十分に残っている。

表�X-7　深海底マンガン団塊鉱床の鉱物資源量
	予測埋蔵鉱量	資源量
仮定採掘限界品位（％、Ni＋Cu）	1.76	0.88
平均品位（％、Ni＋Cu）	2.29	1.57
仮定最低存在量（wet、kg/m2）	5	2.5
仮定平均粒径（cm）*	3.68	3.68
平均存在量（wet、kg/m2）	15	13.5
上記品位･存在量を持つ地域の面積（×106km2）	2.2	18.5
総団塊量（wet、×109 t）	33	250
同上（dry、×109 t）	23	175
仮定ニッケル品位（％）	1.26	0.86
含ニッケル量（×106 t）	290	1,500
仮定銅品位（％）	1.03	0.71
含銅量（×106 t）	240	1,240
仮定コバルト品位（％）	0.25	?
含コバルト量（×106 t）	60	?
仮定マンガン品位（％）	27.5	?
含マンガン量（×9 t）	6	?
平均粒径がこれより小さいと鉱量が減る。例えば2.54cm（1インチ）になるとほぼ30％減少（Archer,A.A.,1979）

　またごく最近には、海洋中の海山の頂きやその山腹に岩石表面を皮殻状に覆って極めてコバルト分に富むいわゆるコバルト･クラストの存在が報告されて、資源的にも極めて注目され出している。しかしまだ発見されたばかりなので、鉱物資源量的な調査はまだ不十分な段階にある。
　海洋地殻表層部でのもう一つ別種の鉱物資源として世界の関心を集めているものにいわゆる熱水成銅･亜鉛鉱床がある。これは主に東太平洋の海洋底中央海嶺付近に発見された極めて特異な産状を示す鉱床である。しかし、まだ調査研究が始ったばかりで、その鉱物資源量推測のための具体的資料に乏しく、まとまった信頼するに足りる量的資料はまだ残念ながら得られていない。この種の鉱床としては、むしろ紅海海底の一部にそれより早く発見された閃亜鉛鉱鉱床の方がずっと詳しく調査されていて、その開発方法すらすでに具体的に研究・準備されている。表�X-8はそこでの鉱物資源量を示したものである。

表�X-8　紅海海底Atlantis �U Deepでの閃亜鉛鉱鉱床の鉱物資源量
Area	Volume (×107m3)	Sp. Gr.	Grade (×103gr/m3)	Metal content (×105t)
�T	36.39	1.56	Zn−4.99 Cu−0.936	Zn−19.9 Cu−3.75
�U	18.95	1.58	Zn−2.05 Cu−0.79	Zn−4.28 Cu−1.54
�V	28.67	1.67	Zn−2.51 Cu−0.835	Zn−32.2 Cu−8.05
Total	84.01	1.60	Zn−3.48 Cu−0.869	Zn−32.2 Cu−8.05 Pb−0.8 Au−45t Ag−4.5×103t
(Hackett,J.P.,Jr. & Bischoff,J.L., 1973)

　これらの資料は表�X-5中にも併記しておいた。その値を同じ鉱種の大陸地殻上部での値と比較すると、特にマンガン･ニッケル・コバルト･銅などの鉱種では、海洋地殻表層部でのそれらの鉱物資源量の値は随分大きい。
　（３）　各種鉱物資源量見積り値の問題点　　　鉱物資源量に関しては多くの研究調査機関あるいは研究者による発表値があるが、それらを理解しあるいは利用するのに当っては、注意して欲しい点がたくさんある。
　a)　見積り値の確からしさ　　　例えば表�X-5には、1980年度での鉄の埋蔵鉱量として93.4×10⁹トン（鉱石中含鉄量、しかもこの場合には脚注によれば回収可能量）、その他の鉱物資源量として104×10⁹トン、既知鉱物資源量として合計197×10⁹トンと記されている。すでに述べたような種々の理由から、これらの数値がすべて3桁の有効数字を間違いなく持っているとは、筆者にはとても考え得られない。従って、ごく一般的には、それぞれを適当に切り上げ・切り下げをして、この場合だったらそれぞれおよそ900億トン・1,000億トン・2,000億トン前後とごくおおまかに理解しておく方が望ましいと考えられる。また金の場合だったら、埋蔵鉱量3.2万トン・その他の鉱物資源量2.9万トン合計既知鉱物資源量6.1万トン程度と理解しておく方が良いだろう。これらの値に対してあまり細かい数値にこだわらない方が良いように思われる。もちろん、埋蔵鉱量中の確測埋蔵鉱量（これまでのいわゆる確定埋蔵鉱量とほぼ同じ内容を持つと考えて良い）の場合には、その確からしさはこれよりずっと良い。
　b)　数値の示す内容　　　広い地域にわたって莫大な資料を集めようとすると、すべてまったく同質のものばかりを集める事は不可能で、集められた個々の資料の質や内容が様々なものになるのは止むを得ない。このため、それらを集計して得た結果に対しては、個々の場合に何らかの内容的制限のつく事も起きて来る。これらはいわゆる註記として表に付記されている。例えば表�X-5にも註記がたくさんついている。この表の値は既知鉱物資源量だが、註記によればその中のある鉱種に対する値の中には潜在鉱物資源量も含まれており、また別の鉱種の場合には、既知鉱物資源量の一部を欠いている。従って、この種の資料の理解・利用に当っては、これらの註記の内容を無視して行うと、場合によっては誤りを生ずる事も十分起り得る。註記の内容は十分正しく理解される必要がある。
　c)　見積りの行われた年次　　　各種鉱物資源量の値は、各年度ごとに変わる量である。例えば埋蔵鉱量の値は、
　（前年度末または年度初頭での埋蔵鉱量）−（その年度での採掘量）＋（その年度での発見量）
だから、それぞれの年度での鉱業活動（探査と採鉱）の大きさ・内容などに様々の影響を受ける。例えば探査活動が鈍って発見量が採掘量を下廻れば、当然の事として埋蔵鉱量は減る。もちろん、その逆の場合も起る。

表�X-9　カナダINCO社のニッケル鉱石年生産量と埋蔵鉱量の変遷
年度	年生産量 ×106t	埋蔵鉱量 ×106t	埋蔵鉱量／ 年生産量比	年発見量 ×106t
1954	13.2	237	18	−
59	13.9	240	17
65	17.9	276	15	17.9
66	15.9	276	17	34.9
67	18.5	295	16	48.5
68	22.6	325	15	33.6
69	17.1	336	20	26.1
70	25.7	345	13	28.7
71	25.0	348	14	28.0
72	17.4	351	20	19.4
73	17.9	353	20	26.9
74		362
1964年度以降はSudburyおよびManitoba両地域の諸鉱山のすべてを含む。年発見量は年生産量と埋蔵鉱量の値より計算。（McAlister,A.L., 1976）

　この関係の1例を表�X-9に示す。この場合には幸いにも、対象地域の地質環境がニッケル鉱床の存在に極めて適しているという地質学的好条件と、同時にそこでの探査活動が極めて活発かつ有効に行われたとの恵まれた2条件が重なり合って、毎年大量の新らしい埋蔵鉱量をつけ加える事が出来た。結果としてこの地域では、将来の15-20年分の生産量に見合うほどの埋蔵鉱量を確保し続けて来た事になる。ただしこのような好条件は何処でも何時でもまたどの鉱種に対しても必らず期待出来るというようなものではない。
　一方、探査の結果未知の土地に新たな有用鉱床を発見する事は、これは言いかえれば、潜在鉱物資源の一部が有用鉱床となり、その結果として埋蔵鉱量が増す事になる。また、技術の進歩や経済条件の大きな変化によって、これまでの経済限界下の鉱床の一部が有用鉱床となり、結果的には既知経済限界下鉱物資源量の一部が埋蔵鉱量につけ加わる事も起る。しかしそれらとは逆に、それまでの粗い探査結果から一応有用鉱床と判断され埋蔵鉱量として計上されていた分が、その後のより詳しい調査によってその相当部分が現在では経済限界下と評価しなおされる場合もある。この場合には埋蔵鉱量の減少となる。
　上のような種々の理由で、各種鉱物資源量の値は毎年再評価される必要があり、見積りの行われた年次が常に必らず付記される必要がある。

　４．　鉱化度
　（１）　McKelveyの経験式　　　私たちが将来とも利用し得る鉱物資源の総量は、いったいどのくらい地殻内あるいはその表層部にあるものなのだろうか。この量については、これまでに何人もの研究者が見積りを行っている。その中で比較的最近になって発表された値は、例えばErickson（1973）やSkinner（1976）の値のように一部を除いて多くの鉱種については少なくとも桁数では一致していて、その間に大きな隔たりは無い（後掲表�X-12参照：略）。このような事情となった一つの理由として、次の事が挙げられよう。
　アメリカ合州国地質調査所長を勤めた事のあるMcKelveyは、1960年に極めて注目すべき内容の論文を発表した。彼によると、アメリカ合州国で当時知られていた各鉱種の埋蔵鉱量（ショート･トン、ｒ）と各元素の地殻存在度（％、A）とを比較してみると、その間にはある一定の規則性が認められて、両者の間には、
　　　ｒ＝A×10ⁿ　　　（n＝6〜11、元素の種類により異なる）
という関係が成り立つという経験式が得られた。そしてこの関係を基とし、またアメリカ合州国の国土面積と全世界の陸地面積（ただし極地方を除く）との比較から各鉱種の世界埋蔵鉱量R（ショート･トン）は、
　　　R＝17.3×A×10^9〜10
で与えられると結論した。McKelveyが経験的に見出したこのR∝Aという関係は、地球科学の立場から見て極めて興味深いものと言ってよいだろう。前に触れたEricksonやSkinnerの得た値は、いずれもこのMcKelveyの経験式での係数や桁数に対して、より新らしい資料を使って考えなおし再計算したものである。
　ところで、上の関係を地球科学の立場からより正しい意味のあるものとするためには、次の点を考える必要があるように思われる。それは、ここに取り上げられた埋蔵鉱量の値は鉱業的な量だという事である。従ってこの値は、各元素の自然的特徴であるそれらの地殻存在度にももちろん何らかの関係を持っているのに違いないが、同時に技術的・経済的などの人為的条件にも大きく関係している筈のものである。そこで、元素の地殻存在度と鉱床に関する何らかの量とが互いに関係しているとするのならば、鉱業的な量に対してではなくて、まず自然の地質学的な量である鉱床量に対して成り立つと考える方が良いと思われる。
　（２）　鉱化度　　　ここでは上の事を考えに入れて、これから述べる鉱化度という考え方に立って、もう一度McKelveyの経験式を考えなおしてみる事としよう（立見辰雄、1979）。
　先に、鉱床とはある特定の鉱物種または化学成分が、普通の岩石の示す変化の範囲を超えて、特に多量に濃集しているような特殊な岩石だと述べた。ここではまずある限られた地域（例えば日本列島・北アメリカ大陸とかあるいは広い面積を占めるある一国の国土とかどれでもよい）を作る地殻部分について、ある元素がどのように分布しているのかを一般的に考えてみよう。この元素は、ここに考える地殻部分を作る多種の岩石中に、種々の鉱物の主成分としてあるいはその中の微量成分としてなどいろいろな形で、少量ずつ広く分散して存在しているだろうし、またその一部は、この元素（現実にはそれを多く含む鉱物）の鉱床を作って局部的に濃集もしているだろう。今この元素iのこの地殻部分に存在している全量をti（トン）とし、そのうちで鉱床となって濃集している分をri（トン）とした時、ri/tiの比をこの元素のこの地殻部分での鉱化度と呼ぶ事とする。別な言い方をすれば、今考えている地殻部分はこの元素に関してどのくらいの強さで鉱化されているかの度合いをこの比の値が示すという事になる。
　上の事をより一般化して表わせば、次のようになる。ある与えられた質量m（トン）を持つ地殻部分についてのある元素i（その大陸地殻存在度をAi(ppm)とする）の鉱化度mfiは、この地殻部分に存在する元素iの全量をti（トン）とし、そのうち鉱床となって濃集している分をri（トン）とすれば　mfi＝ri/ti　で表わされる。今ここで、ここに考える地殻部分がある程度以上に大きくて、そこを作る多種岩石中の分散して存在している元素iのこの地殻部分全体を通じての平均的な存在度は、この元素の大陸地殻存在度の値で代表され得ると考えられるような場合に限るとすれば、
　　　ti＝m（トン）・Ai（ppm）・10^-6（トン）
なので、従ってこの場合の鉱化度は次式で与えられる。
　　　mfi＝ｒi/m・Ai・10^-6
　（３）　地域別鉱化度
　a)　一つの具体例　　　南アメリカ大陸太平洋岸アンデス山脈地域は、そこでの地質環境の特質上、銅の鉱化作用の強さという点では、世界的に優れた地域の一つに算えられている。この地域には、これまでに多くのしかも大規模な銅鉱床が発見・稼行されており、現にチリ・ペルーの2ヶ国は世界でも有数の銅鉱石産出国である。1978年度での全世界銅鉱石生産量（鉱石中含銅量）のおよそ20％はこの2ヶ国で占められた。また、全世界（ユーゴスラビアを含み、他の共産圏諸国を除く）の銅埋蔵鉱量（鉱石中含銅量、1979）中でラテンアメリカ諸国の占める割合いは、実に35％を超えると、見積られており（鈴木昌也ほか、1980）、その大部分はこのアンデス山脈地域に在る銅鉱床によっている。
　この地域に知られる各種の銅鉱床の中では、斑岩銅鉱床と呼ばれる型式のものが、一つ一つの鉱床の規模も大きくかつ発見された鉱床の数も多い。北はコロンビアから南はチリ中央部に到るまでのこの地域の斑岩銅鉱床については、探査も比較的に良く進んでいて、1978年にHollisterが発表した資料によると、この地域の主な斑岩銅鉱床全体の埋蔵鉱量（鉱石中含銅量）は約1.7億トンと見積られている。この地域にはもちろん他の型式の銅鉱床もたくさん知られているが、それらの規模は斑岩銅鉱床のそれにくらべれば一般には小さいので、この値をこの地域でのすべての既知有用銅鉱床中に濃集している銅の総量と見なしても、第1近似としてはそれほど大きな誤りは無いと考えてもよいだろう。もちろん、この地域の真の銅の鉱化度を知るためには、既知・潜在あるいは有用・経済限界下のいずれをも問わず、この地域に存在しまたは存在するであろう各種の銅鉱床すべての中の含銅量を考え、さらにそれらの既採掘量をも併せ考えなければならないのだが、それらに関する具体的資料を得る事はむずかしいので、今は取りあえずこの値を基に考えるよりほかに方法がない。
　一方、ここで考えるある限られた範囲の地殻をどのくらいに考えたら良いのかは、本来ならば南アメリカ大陸太平洋岸アンデス山脈地域の地質環境や地質構造を具体的に調べ上げた上で、この問題を考えるのに適当と考えられる範囲を決める必要がある。しかしここではごくおおまかに考えて、南北4,500キロメートル・東西200キロメートル・深さ5キロメートル（表面積は9×10^5平方キロメートル、日本の2.5倍弱）の範囲の地殻部分を考える事としよう。この地殻部分内にはもちろん極めて多種の地層･岩体が分布し、複雑な地質構造を作って重なり合っている。またそれぞれの岩石種ごとにその平均含銅量も幅広く変っている。しかし、この程度の大きさの地殻部分を1単位として考えるとすれば、この地殻部分全体を通じての銅の平均存在度としてその大陸地殻存在度の値55ppmをとっても、少なくとも第1近似としては、許されよう。このように考え、かつこの地殻部分の平均比重を2.7として試算すれば、この地殻部分内に存在する銅の全量は6.7×10¹¹トンとなる。
　ここで、この地殻部分内で鉱床を作って濃集している銅量として先の1.7×10⁸トンを考えれば、ここでの銅の鉱化度はr/t＝2.5×10^-4となる。今ここに1例として考えて来た南アメリカ大陸太平洋岸アンデス山脈地域の大陸地殻上部（深さ5キロメートル）では、すでに述べたようにこの地域が世界でも有数の銅鉱石産出地域または銅の埋蔵鉱量も極めて大きい地域、すなわち銅の鉱化作用の強い地域と考えられるのにもかかわらず、そこに存在する全銅量のうち僅か0.025％に相当する分しか鉱床を作って濃集していないという事になる。鉱床というものが如何に特殊な岩石であるかは、この事からも判って頂けるだろう。もちろん、これまでに注意して来た多くの事から考えれば、ここに得たこの地殻部分での銅の鉱化度としての2.5×10^-4という値は、決して真の鉱化度の値ではなく、いわば現在試算し得る範囲内での最小値であるのにすぎない。
　b)　世界各地域での個別的鉱化度　　　最近世界各国の国別または地域別の各種鉱物資源の埋蔵鉱量あるいは一部では他の鉱物資源量の値が発表されて来ており、いくつかの国または地域ごとの個別的な鉱化度を試算出来るようになった。その結果を表�X-10として示す。これらはいずれも、深さ5キロメートルまでの大陸地殻上部を考え、そこでの平均の比重を2.7と仮定して試算してある。実は本来ならまず最初には、国別という人為的な囲いではなくて、地殻の長い歴史の特徴をそれぞれに反映している特定の地質構造区あるいは鉱床区などと言った地質学的な構造区分ごとに、それぞれの鉱化度を試算したいのだが、それに適した基礎資料は極めて少ないので、ここでは主に国別で行うのも現状では止むを得ない。この意を少しでも表わそうと思って、表�X-10に載っている各国別の鉱化度は、若い構造帯（日本･メキシコ）・多くの異った地質環境を含む大陸（北アメリカ･オーストラリア・カナダ）・先カンブリア時代楯状地（カナダ・南ア共和国内のそれぞれ一部地域）と大分無理して分けてある。ただし先カンブリア時代楯状地に関するものは、原資料ですでにその国の中でのこの地質構造区に属する地域のみについての資料が発表されているものである。

表�X-10　地域別鉱化度
	大陸 地殻 存在度 (Mason, 1966) (ppm)	大陸地殻上部*1	若い構造帯		大陸				先カンブリア時代楯状地
			日本*2	メキシコ*3	北アメリカ大陸*4 (アメリカ合州国＋カナダ)		オーストラリア*5	カナダ*6	カナダ*7	南ア共和国*8
		M=2.25×1019t n=0.2	3.7×105km2 5.0×1015t	1.97×106km2 2.66×1016t	1.9×107km2 2.6×1017t		7.69×106km2 1.04×1017t	9.98×106km2 1.35×1017t	2.3×106km2 3.1×1016t	1.22×106km2 1.65×1016t
		既採掘量＋ 埋蔵鉱量(80)	既採掘量＋ 埋蔵鉱量(60)	確認埋蔵鉱量(78)	埋蔵鉱量(80) A	総鉱物資源量(80) B	埋蔵鉱量(75)	埋蔵鉱量(76)	既採掘量＋ 埋蔵鉱量(78)	既採掘量＋ 総鉱物資源量(80)
Fe	50,000		2.7×10-7	1.3×10-7	1.1×10-5	3.4×10-5	3.4×10-6			3.2×10-6
Mn	950		7.1×10-7	1.3×10-6		3.6×10-6	5.0×10-6			2.4×10-4
Cr	100		1.1×10-6							2.8×10-4
Ni	75	2.5×10-7			4.6×10-6	1.9×10-5	2.4×10-7	7.9×10-7	6.6×10-6	1.9×10-5
Co	25		1.6×10-7		4.6×10-8	1.6×10-6			1.5×10-8
W	1.5		2.6×10-6		1.0×10-5	2.7×10-5	3.9×10-7
Mo	1.5		1.0×10-6		1.4×10-4	2.6×10-4		6.7×10-6
Ti	4,400				5.2×10-7	1.5×10-6
Cu	55	2.9×10-6	2.3×10-5	1.5×10-5	8.7×10-5	3.6×10-4	1.0×10-6	3.7×10-6	1.2×10-5	2.8×10-5
Pb	13	5.4×10-6	2.0×10-5	1.4×10-5	1.2×10-4	3.1×10-4	1.0×10-5	8.5×10-6		3.1×10-5
Zn	70	1.3×10-6	3.0×10-5	1.6×10-6	2.5×10-5	7.0×10-5	2.7×10-6	4.6×10-6	9.6×10-6	1.4×10-5
Sn	2		5.9×10-6		1.3×10-6	7.7×10-6	1.6×10-6
Sb	0.2		7.0×10-5		3.3×10-5	3.8×10-5	3.8×10-6			2.1×10-4
Mg	0.08		1.7×10-5		7.8×10-6	1.9×10-5
Au	0.004	6.8×10-6	3.1×10-5		1.7×10-5	9.1×10-5	3.8×10-7	4.5×10-6	3.4×10-4	7.8×10-4
Ag	0.07		3.4×10-5	1.3×10-5	5.3×10-5	1.5×10-4	3.3×10-6	1.6×10-5	1.0×10-5	6.6×10-6
Pt gr	0.01				1.1×10-6	3.0×10-6				3.8×10-4
U	1.8	3.9×10-7		2.1×10-6	9.2×10-7	1.3×10-6	1.4×10-6		1.2×10-5	1.8×10-5
Al	81,300				4.7×10-9	2.4×10-8	3.5×10-7
計算の基礎とした各種鉱物資源量に関する資料はそれぞれつぎによる−*1：別表�X-4、*2：関根(1962)、*3：EIR(1980)、*4：USBM(1981)、　*5：Aust.B.M.R., Miner.Res.Sect.(1975)、*6：McKintosh,J.A. & Crauston,D.A.(1977)、*7：Derry,D.R.(1980)、*8：Van Biljon,W.J.(1980)

　表�X-10に示されている国別または特殊地域別の鉱化度の値（後の述べるように真の鉱化度ではなく、現在試算し得る最少値）は、地質学的には次のような意味を持っている。
　i)　北アメリカ大陸（ここでは便宜上アメリカ合州国とカナダを合せた地域）とした地域には、時間的には始生代から新生代にかけてのおよそ40億年近くにもわたり、かつ地質学的にはそれぞれ性質を異にする各種の地質環境より成る多くの地域、つまり多種の地質構造区や鉱床区を含む地域が、極めて広い面積（1.9×10⁷平方キロメートル、日本の約50倍）の土地の中に含まれている。従って、その全域に対して得られる鉱化度の値は、大陸地殻上部を通じて眺めるという立場からすれば、他の例にくらべてより平均的な値を示す例と考えて良いだろう。
　ii)　オーストラリア・カナダ・南ア共和国の各国は、ソ連邦やアメリカ合州国などと共に、世界的に見て鉱物資源に富む国々である。地質学的には、先カンブリア時代（今からおよそ40-6億年前の期間）に出来た各種の地層･岩石より成るいわゆる楯状地が、その国土の中で大きな面積を占めている点に、その第1の特徴がある。と同時にそれぞれの一部には、より若い地質時代の地質環境より成る部分も含まれている。一般的には、世界的に見て各種の鉱化作用（鉱床を作る種々の地質作用）、特に先カンブリア時代のそれ、の著るしい地域の例と見なす事が出来る。なお先に述べたように、カナダおよび南ア共和国の場合には、先カンブリア時代の地層･岩体より成る地質構造区（楯状地）中の鉱床のみを対象とした各種鉱物資源量の値も発表されているので、それらは別に取り扱われている。
　iii)　日本･メキシコの両国は、地質学的に見れば前記各国とは対照的に、主に古生代以降（6億年前より現在までの期間）のより若い地質時代の地層･岩体より成っており、地殻の歴史の中では若い時代の鉱化作用に富む地域の例と考えてよいだろう。
　c)　個別的鉱化度見積り値に見られる特徴　　　なおここで、これらの資料を読む場合に気をつけて欲しい点をまず記しておこう。それは、この試算を行うのに当って利用し得た基礎資料は、本来ならば｢鉱床を作って濃集している分の全量｣の真の値であるべき筈だが、この値は現在ではまだ何も判っていないので、次善の策として現在判っている各種鉱物資源量の具体的数値資料を使わざるを得なかったという事である。しかも現実には、種々の事情から国や地域によって次のようにいろいろな場合がある。
　既採掘量＋埋蔵鉱量の値を利用したもの−日本、カナダ先カンブリア時代楯状地
　既採掘量＋総鉱物資源量の値を利用したもの−南ア共和国先カンブリア時代楯状地
　総鉱物資源量の値を利用したもの−北アメリカ大陸B
　埋蔵鉱量の値を利用したもの−北アメリカ大陸A、オーストラリア・カナダ
　確認埋蔵鉱量の値を利用したもの−メキシコ
　このように、試算に使われた基礎資料の質に広い差があるので、得られた結果としての諸数値を比較検討する場合には、この点を十分考慮に入れる必要がある。古くから利用されあるいは近代産業の基礎原料としてここ200-100年以降大量に使われて来た鉱物資源の場合には、いずれも既採掘量の値は極めて大きく、これを計算に入れるかどうかは、結果に相当の影響を与える。また北アメリカ大陸Bや南ア共和国先カンブリア時代楯状地の場合のように、埋蔵鉱量のみでなく他の各種鉱物資源量も含まれている数値を使えば、当然の事ながら他の場合よりも大きな鉱化度の値が得られる。いずれにせよ、ここに与えられた各国・各地域の鉱化度は、いずれも真の値ではなくて、いろいろな意味合いを持つみかけの値あるいは現段階で一応数値化する事の出来た最小値というべきものである。
　以上述べて来た事を踏えた上で、表�X-10に示されている結果から読みとれる事は次の諸点であろう。
　i)　ここに挙げた8地域・29鉱種に関しては、同一地域では10^-6から10^-9（北アメリカ大陸A）、特定鉱種については10^-4-10^-7（金･マンガン）と大きく変わる例から、それほど変らないもの（亜鉛、10^-5-10^-6）まで、いろいろな場合がある。これは、対象とした地域の地質環境にはそれぞれの場合ごとに大きな違いがあり、そこでの地史も違っている事、ならびに、鉱種によりまた鉱床型式によってもそれらの生成に都合の良い地質環境を異にし、また規模も違う事との二つの事情から、地域別鉱化度や鉱種別鉱化度の値にそれぞれ大きな差を生じる事は、地質学的にはそれぞれに十分な理由があると考えられる。ただし亜鉛の場合のようにその鉱化度の値が各地域間で比較的狭い幅しか示さない事については、はっきりした理由がまだ見出し得ない。
　ii)　日本列島の場合には、鉄・マンガンなど少数の例を除けば、多くの鉱種に対して鉱化度の値は10^-5-10^-6の範囲にあり、ここに挙げられた諸例の中では極めて平均的な値である。つまり、鉱化作用の強さの度合いという点では、日本列島は決して世界的に見て弱くはない。これを北アメリカ大陸Aの場合と比較したのが図�X-5である。これを見ればすぐ判るように、亜鉛・錫・アンチモン・コバルト･金などの鉱種に関しては、日本の場合の方が北アメリカ大陸での値よりも高い。これは日本列島がその変化の多い地史の中で極めて複雑な地質構造を持つに到った事の反映であって、この列島の地質学的特徴の一つを示す事実である。しかし一方、日本は鉱物資源に乏しい国と言われ、実際に近年では自国産業を支えるために毎年世界各地から多種・多量の鉱産物を輸入している。これは、比較的恵まれたとも言える自然条件−ここでの鉱化作用の度合いは決して弱くはない（ただし国土面積はそれほど広くはないから鉱床量の絶対的な大きさには限りがある）−に対して、近年の国内産業の著るしい発達に伴って、その需要量が段違いに大きくなりすぎてしまった事を意味している。

図�X-5　地域別鉱化度（別ウィンドウに拡大）

　iii)　カナダ・南ア共和国の先カンブリア時代楯状地では、一部の鉱種を除いて他の大部分のものに対しては、鉱化度の値は10^-4-10^-5であって、他地域に対してのものより1桁大きい。これらの場合、共に既採掘量の値が計算に含まれており、また南ア共和国の場合には総鉱物資源量を基にしているので、これらがこの大きな値を与える要因になっているのは確かであろう。しかしこの点を考慮外としてもなおかつ、これらの地域での鉱化度の値は他地域での値より一般に大きいと考えて良いだろう。言いかえれば、これらの地域は鉱物資源に富む能力を持っている。これは、先カンブリア時代楯状地の地質学的特徴の一つの表われと言っても良いだろう。
　（４）　大陸地殻上部での各元素に共通した平均の鉱化度　　　これまでは、基礎資料の得られた各地域について、いくつかの選ばれた元素に関する個別的鉱化度の値を求めて来た。この章での目的である｢大陸地殻上部にはどのくらいの総鉱床量が見積られ得るのか｣という問題に対しては、次に大陸地殻上部での各元素に共通した平均の鉱化度の値を知る必要がある。もちろん、各元素（鉱種）に関する鉱化度が大陸地殻上部に対して｢共通の平均値｣を持たなければならないという理論的根拠はまだ得られていない。むいろ、これは元素ごとに値を異にすると考える方が正しいかも知れない。しかしここでは、おおずかみな見当をまずつけるという観点から、差し当たりの第1歩としてそのような値が考えられ得ると仮定して、話を先に進める事としよう。
　これを考えるのに当ってまず第1に注目すべき事は次の点である。すでに述べたように、銅･鉛･亜鉛・ニッケル・金･ウランの6鉱種については、世界全体での埋蔵鉱量と共に、その既採掘量も見積られている。これら両者の値を基にし、古くから利用されかつその探査もよく進んでいると考えられる銅･鉛･亜鉛・金の4鉱種について、それらの大陸地殻上部での鉱化度を試算すると、表�X-11の結果を得る。それらの値は1.3-6.8×10^-6の範囲にあり、すべて10^-6の桁である。なお、ウランとニッケルのそれは10^-7の桁となっている。

表�X-11　古くから使われて来た金属元素の大陸地殻上部での鉱化度
鉱種	既採掘量*1 −1979、×108 ｔ	埋蔵鉱量		既採掘量＋埋蔵鉱量
		1980、×108 t*2	鉱化度	1980、×108 t	鉱化度
Cu	2.32	4.94	2.0×10-6	7.26	2.9×10-6
Pb	1.81	1.27	2.2×10-6	3.08	5.3×10-6
Zn	2.32	1.62	5.1×10-7	3.94	1.3×10-6
Au	9.0×104	3.23×104	1.8×10-6	1.22×105	6.8×10-6
Ni	0.12*3	0.73*3	2.2×10-7	0.85	2.5×10-7
U	0.57	2.59×106	3.2×10-7	3.16×106	3.9×10-7
*1　表�X-4、*2　USBM,1981、*3　Riss,J.R. & Travis,G.A.,1981、この試算では大陸地殻上部に対して、M＝2.25×1019 t、n＝0.2をとってある。

　第2に、1地域内に種々の地質環境を含んでいて、平均的な鉱化度の値を考える上で得られた結果の中では最も都合の良いと思われるものは、北アメリカ大陸のそれである。この場合には、特殊な例（例えばアルミニウム）を除いては、大部分の元素に対して埋蔵鉱量だけを基に試算した場合に10^-6-10^-4程度、これにその他の鉱物資源量をも加えて試算した場合でも同じく10^-6-10^-4程度である。
　第3に、地域別鉱化度として得られた値の中で特に高い10^-4の桁を持つ例は、南アフリカ共和国先カンブリア時代楯状地（基礎資料は既採掘量＋総鉱物資源量）でのマンガン･クロム・金･白金・アンチモン、カナダ先カンブリア時代楯状地（同じく既採掘量＋埋蔵鉱量）の金、北アメリカ大陸B（同じく総鉱物資源量）の銅･鉛･モリブデン･銀および北アメリカ大陸A（同じく埋蔵鉱量のみ）の鉛･モリブデンの各元素である。これら諸地域の地質環境は、上に挙げられた諸元素の鉱床を作るのに適した特有の性質を持っている事が、これまでの地質学的な調査・研究によってよく判っており、このような高い値を示す事は十分に良く理解出来る。例えば、南ア共和国ブッシュフェルト地域のクロム・白金の鉱床やウィットウォータースランド地域の金鉱床、あるいはアメリカ合州国のミシシッピ型鉛･亜鉛鉱床やロッキー山脈地域の銅･モリブデンまたはモリブデンの斑岩型鉱床などは、世界的に見て最大規模の鉱床の好例として挙げられるものである。しかし、このような高い鉱化度の値をそのまま簡単に大陸地殻上部全体にまで及ぼして、この値をそれらの平均的な値とみなす事は、例え潜在鉱床がまだまだ見つけられ得る事を十分予測するとしても、地質学的には楽観的な見方と言っても良いように考えられる。
　最後に、すでにはっきり示しておいたように、ここに挙げられた鉱化度の値は、いずれもそれぞれの場合ごとに試算された最小値であって、真の鉱化度の値はそれらより大きい筈という事である。
　以上の諸条件を基礎として考えると、大陸地殻上部での各元素に共通した平均の鉱化度の値としては、第1および第2の事実で得られた10^-6前後の値をまず基礎として考え、それらに第3・第4の事実をも考えに入れてその少なくとも10倍、せいぜい100倍程度、すなわち10^-5-10^-4の桁を採るのが、現在の知識としては妥当ではないかと考えられる。このうち高い方の値（10^-4の桁）を考えるのは、すでに記したようにどちらかと言えば楽観的な見方と言って良いだろう。

　５．　総鉱床量の見積り
　（１）　大陸地殻上部　　　ここで、鉱化度とは何であったかをもう一度思い出して頂こう。鉱化度（mfi）とはある限られた地殻部分（質量mトン）中に存在するある元素i（その大陸地殻存在はAi ppm）の全量をtiトン、そのうち鉱床となって濃集している分をriトンとした時、mfi＝ri/ti　で与えられるものである。今ある程度以上の大きさを持つ地殻部分を対象として考え、第1近似としては　ti＝m・Ai・10^-6（トン）が成り立つような場合には　mfi＝ri/m・Ai・10^-6　となる。これを変形すれば、
　ri＝m・Ai・10^-6・mfi　（トン）
が得られる。
　次にこれを大陸地殻上部全体にまで押し進めて考える事にしよう。大陸地殻全体の質量をMトン、そのうち大陸地殻上部の占める範囲（実際には、将来とも固態鉱物資源の採掘の及び得ると期待される範囲）の大陸地殻全体に対する割合いをn％、大陸地殻上部を通じての各元素に共通した平均の鉱化度をMF、各元素iの大陸地殻存在度をAi（ppm）とし、ある元素iが大陸地殻上部で鉱床を作って濃集している分の総量（その元素の大陸地殻上部での総鉱床量）をRiトンとすれば、前式から、
　Ri（トン）＝M（トン）・0.n・Ai（ppm）・10^-6・MF
となる。ここで、
　M＝22.5×10¹⁸トン、MF＝10^-4または10^-5、
　n＝0.2または0.3（大陸地殻の平均の厚さを仮に平均35キロメートルとすれば、地表からの深さで7-10キロメートル前後までの範囲）
として計算すれば、次の4式を得る。
　A．　Ri＝6.8Ai×10⁸　（トン）（〔MF〕＝10^-4、n＝0.3）
　B．　Ri＝4.5Ai×10⁸　（トン）（〔MF〕＝10^-4、n＝0.2）
　C．　Ri＝6.8Ai×10⁷　（トン）（〔MF〕＝10^-5、n＝0.3）
　D．　Ri＝4.5Ai×10⁷　（トン）（〔MF〕＝10^-5、n＝0.2）
例えば銅についてACu＝55ppmとして試算すれば、
　RCu＝3.7×10¹⁰、2.5×10¹⁰、3.7×10⁹、2.5×10⁹　（トン）
を得る。これは、大陸地殻上部（地表からの深さ7-10キロメートルまでの範囲）での銅の総鉱床量（目的成分含有量）は、きつく見積って約25億トン、ごく緩く見積ればおよそ370億トン前後ありそうだという事を意味している。しかし、これでは見積り値とは言えあまりにも大きな幅がありすぎて、このような試算にどれだけの意味があるのかと疑問に思われる人も多いかも知れない。もちろんこれらの値は、現在私たちが持っている地球や岩石・鉱床などについての基礎知識を基にし、それに多くの仮定を置いた上で試算した値であって、まだまだ不正確な点の多いものである事に間違いはない。しかし現在の知識を基にしての一つの具体的な解答ではある。今後の問題は、このような事を考えかつそれを具体的に試算するのに必要な地球科学上の基礎研究を進めると共に、必要な基礎数値資料をより精しくかつ正確に求め、また仮定事項の内容をさらに十分吟味しなおして、より真に近い値を求め得るよう努力する事にあろう。

表�X-12　大陸地殻上部での総鉱床量および鉱物資源量の見積り

鉱種

大陸地殻存在度*1 (ppm)

大陸地殻上部

鉱物資源量（ｔ）

総鉱床量(t)*2

鉱物資源量(t)

大陸地殻上部(1980)*6

海洋地殻表層部*7 (1979)

A

D

F*3

E*4

S*5

既採掘量(〜'79)（A)

埋蔵鉱量

その他

計(B)

A＋B

Fe

50,000

3.4×1013

2.3×1012

1.3×1011

2.0×1012

−

9.34×1010

1.04×1011

1.97×1011

Mn

950

6.5×1011

4.3×1010

5×108

4.2×1010

−

1.36×109

1.45×109

2.81×109

6.0×109

Cr

100

6.8×1010

4.5×109

7×108

3.3×109

−

3.36×109

2.93×1010

3.27×1010

Ni

75

5.1×1010

3.4×109

5×107

2.6×109

1.2×109

1.16×107

6.00×107

1.68×108

2.28×108

2.40×108

2.9×108

Co

25

1.7×1010

1.1×108

3×106

7.6×108

−

2.40×106

3.04×106

5.44×106

6.0×107

Mo

1.5

1.0×109

6.8×107

4×106

4.7×107

2.0×107

9.48×106

1.14×107

2.09×107

W

1.5

1.0×109

6.8×109

1×106

5.1×107

1.7×107

2.59×106

4.17×106

6.76×106

Ti

4,000

3.0×1012

2.0×1011

−

2.3×1011

−

2.73×108

4.24×108

6.97×108

Nb

20

1.4×1010

9.0×108

−

−

3.4×108

4.08×106

1.31×107

1.72×107

Be

2.8

1.9×109

1.3×108

−

6.4×107

−

3.80×105

7.3×105

1.1×106

Cu

55

3.7×1010

2.5×109

2.5×108

2.1×109

1.0×109

2.32×108

4.94×108

1.13×109

1.63×109

1.86×109

2.4×108

Pb

13

8.8×109

5.9×108

1.5×108

5.5×108

1.7×108

1.88×108

1.27×108

1.61×108

2.88×108

4.76×108

Zn

70

4.8×1010

3.2×109

2.5×108

3.4×109

−

2.33×108

1.62×108

1.63×108

3.25×108

5.58×108

3.2×106

Sn

2

1.4×109

9.0×107

7×106

6.8×107

2.5×107

1.00×107

2.70×107

3.70×107

Sb

0.2

1.4×108

9.0×106

−

1.9×107

−

4.36×106

8.1×105

5.17×106

Ga

15

1.0×1010

6.8×108

−

−

−

1.10×105

5.5×104

1.65×105

Au

0.004

2.7×106

1.8×105

3×104

1.5×105

3.4×104

9.0×104

3.23×104

2.90×104

6.13×104

1.51×105

Ag

0.07

4.8×107

3.2×106

−

2.8×106

1.3×106

2.53×105

5.17×105

7.70×105

4.5×103

Pt

0.01

6.8×106

4.5×105

−

1.2×106

8.4×104

3.67×104

6.33×104

1.00×105

U*8

1.8

1.2×109

8.1×107

1×106

9.3×107

2.7×107

4.7×105

1.75×106

3.27×106

5.02×106

Al

81,300

5.5×1013

3.7×1012

2×109

3.5×1012

−

4.72×109

3.31×109

8.03×109

Mg

20,900

1.4×1013

9.4×1011

−

−

−

2.79×109

9.5×108

3.74×109

P

1,050

7.1×1011

4.7×1010

7×109

5.1×1010

−

3.45×1010

9.5×1010

1.30×1011

K

25,900

1.8×1013

1.2×1012

4.3×1010

−

−

7.55×109

1.12×1011

1.20×1011

(数値は鉱床・鉱石中の目的成分含有量、ただしクロム・燐は鉱石量。) *1：Mason,B.(1966)、*2：立見(1979)を改定、*3：Friedensburg,F.(1957)“予想開発鉱量”、地表より3km以浅、*4：Erickson,R.L.(1973)“回収可能資源量”、4.2A(ppm)×107(t)、*5：Skinner,B.J.(1976)深さ10kmまでの大陸地殻中の全金属量の0.01％が採鉱・選鉱可能な鉱物中に存在と仮定、*6：USBM(1981)その他の大部分は既知鉱物資源量、一部に潜在鉱物資源量を含む、*7：マンガン･ニッケル・コバルト･銅はArcher,A.A.(1979)亜鉛・銀はHackett,j.P.,Jr.& Bischoff,J.L.(1973)、*8：鉱物資源量はOECD/IAEA−NEA(1981)、共産圏を除く。

　上のような考えを基にして、適当に選ばれた24種の鉱物資源について大陸地殻上部での総鉱床量（目的成分含有量で示す）を試算した結果が、表�X-12と図�X-6とである。総鉱床量を計算する式がよく示しているように、この値はそれぞれの元素の大陸地殻存在度の値に比例しているのだから、この存在度の大きい元素ほど総鉱床量も大きくなる。この24鉱種の中では、最大の見積り値はアルミニウムの5.5×10¹³ないし3.7×10¹²トン、最少の見積り値は金の2.7×10⁵トンないし1.8×10⁵トンとなっている。なお表�X-12には、比較のためにこれまでに発表されている大陸地殻上部での総鉱物資源量に関する見積り値3種、および大陸地殻上部と海洋地殻表層部での各種鉱物資源量とを掲げておいた。
　これらの表や図を読めば判るように、多くの元素については、これまでに見積られた大陸地殻上部での各種鉱物資源量の総和（一部のものについては既採掘量も含めてある）は、一般には最少の総鉱床量見積り値Dよりも大分小さく、まだまだ十分な余裕があるように見える。ただしこれは、総鉱床量見積り値（地質学的な量）との比較であって、そのうち実際に将来利用し得ると見込める量（鉱業的な量）がどれだけかはまた別に考えなければならない問題であり、それは後に考える事とする。
　しかしその点を考慮したとしてすら、銅･鉛･金の場合には、それらの既採掘量と大陸地殻上部での各種鉱物資源量との総和は、それぞれの総鉱床量D値に対して0.74・0.81・0.84の割合いを占め、極めて近くなっている。このほか、錫・アンチモンの場合には既採掘量の値が知られていないのにも拘らず、その比は0.41・0.57となっており、既採掘量をも含め得るとすれば、上の3種の場合と似た割合いになる可能性が大きい。このような関係は次のような疑問を起させる。
　i)　これらの元素については、もう総鉱床量D値に対してぎりぎりまたはそのごく近くまで、その存在量を地質学的に確認または推定してしまったのか
　ii)　あるいは、試算の基礎とした各元素に共通した平均の鉱化度という考えに誤りがあって、本来ならば各元素ごとに異る鉱化度を別々に求めた上で試算しなければならないのか、言いかえれば、銅･鉛･金などについては総鉱床量D値を小さく見積もりすぎたのではないか
　iii)　また場合によっては、上とは逆に各種鉱物資源量の見積りに甘すぎる点があるのではないだろうか
などの点である。ここでは差し当り、上のような問題のある事は残した上でi)の立場をとる事として話をさらに進める事にしよう。
　（２）　海洋地殻表層部　　　近年での活発な海洋調査の結果、海洋底にも何種類かの鉱床の存在している事がしだいにはっきりして来た。例えば、大洋深海底でのニッケル・コバルト･銅など各種の金属に富むマンガン団塊鉱床や紅海海底の海盆中の閃亜鉛鉱鉱床などについての実態が知られるようになってもう随分年数が経った。これらについての既知鉱物資源量についてはすでに数値を挙げておいた。また最近では、東太平洋中央海嶺付近の海底で銅･亜鉛などの硫化鉱物を主とするいわゆる熱水成非鉄金属鉱床が各地に発見・研究され、また太平洋海底の海山の頂きや山腹斜面には、コバルト分に富む極めて特殊な皮殻（コバルト･クラスト）が岩石表面に付着して鉱床を作っている事も発見・報告されている。これらも将来の鉱物資源として大いに期待されているが量的な調査・研究はまだまだ進んでいない。これら深海底に在る各種鉱床の探査は、陸上の場合と違って多くの困難を伴っているので、詳しい事はまだよく判っていない。少なくとも、海洋地殻表層部での総鉱床量を具体的に試算するのに必要な具体的数値資料は、まだ極めて不十分である。
　ごく一般的に言えば、現在の海洋地殻の歴史は大陸地殻のそれにくらべればずっと新らしく、かつその地質構造もより簡単なので、そこに存在するであろうと地質学的に推定し得る各種鉱床の種類･型式は、大陸地殻中でのそれよりずっと少ないだろうと考えられる。

図�X-6　大陸地殻上部での総鉱床量および鉱物資源量。（別ウィンドウに拡大）

　６．　総鉱物資源量の見積り
　（１）　総鉱床量のうちどれだけが鉱物資源として利用し得るか　　　これまでは、ある特定の鉱物種または化学成分の鉱床について、大陸地殻上部に存在するであろうすべての鉱床中に、それらがどのくらいの量濃集しているのか、すなわち総鉱床量を見積ってみた。しかし、この量のすべてが直ちに将来とも実際に利用可能な鉱物資源量と考えてよいのかどうかは、改めて十分に考えてみる必要がある。
　天然に産する鉱床を実際に探査・開発･利用するためには、私たちはこれに多くの技術的・経済的その他の働きかけを行う必要がある。しかも、現在または近い将来の事だけではなくて、将来何10年もあるいはそれ以上もの長い先にはどこまで働きかけ得るようになるのだろうかとの見透しも立てなければならない。例えば、
　i)　将来とも地表面下・海面下または海底面下何キロメートルの深さのところまで鉱床探査を具体的に行い、かつ評価に必要な資料・試料を得る事が出来るようになるのだろうか。（探査・評価）
　ii)　将来とも地表面下・海面下または海底面下何キロメートルの深さのところまで固態鉱物資源の採掘を実際に行えるようになるのだろうか。（採掘）
　iii)　将来とも採掘限界品位や粗鉱平均品位などをどの程度まで下げ得るようになるのだろうか。（採鉱・選鉱）
　iv)　将来とも製錬給鉱品位はどの程度にまで下げ得るようになるのだろうか。また製錬可能な鉱物の種類を現在以上にどれだけ増す事が出来るようになるのだろうか。（製錬）
　v)　鉱業諸工程での実収率を将来ともどの程度にまで上げ得るのだろうか。
　vi)　鉱業諸工程で必要なエネルギー量を将来ともどの程度にまで下げ得るのだろうか。またこれに必要なエネルギーを望む時に何時までも十分に確保出来るのだろうか。
　vii)　将来の鉱産物の需要量や価格に関連して、将来の社会生活･産業活動の構造あるいは人口増加などはどのように変化するのだろうか。
　viii)　鉱業諸工程に伴う廃棄物処理はどのようにしたらよいのか。
などの諸問題の見透し如何によって、将来とも利用可能となるべき鉱物資源量の見積り値は大きな影響を受ける。もちろん、私たちはこれらの点についての調査・開発にこれまで大きな努力を払い続けて来たし、また将来も続けるだろう。それで、少なくとも抽象的に言えば、まだここ暫くの間は、まだまだより深いところまで、またより低品位の鉱床をも、探査・開発･利用出来るだろう事に間違いはない。しかし一方で、種々の理由からこれらが無制限に続き得るものとも考え難い。
　上に挙げた諸条件のすべてについてここに具体的な見透しを立てる事は、明らかに筆者の能力を遙かに越えている。従って、この項のまとめとして今言える事は、少なくとも鉱床を唯一の源として考えるような鉱物資源に対しては、これまでに考えて来た総鉱床量の値は、考え得る総鉱物資源量の最高値、どんなに努力しても超える事の出来ない自然的な制限という事に止る。
　（２）　鉱物学的障壁　　　上に挙げた多くの問題点の中で鉱業に必要なエネルギーに関連しては、すでに第4章の一部で少しだが触れておいた。ここには鉱物的な問題点を少し考えてみる事にしよう。
　鉱物中のある特定成分を抽出・利用する場合に現在利用されている鉱物の種類はたくさんあるが、その大部分は比較的に言って化学的に分解し易い酸化鉱物・硫化鉱物・炭酸塩鉱物などの種類のものである。これに対して、珪酸塩鉱物・含水珪酸塩鉱物の中で現在よく利用されているものは、テフロ石（Mn2SiO4−Mn）・ベルトランダイト（Be4Si2O7(OH)2−Be）・緑柱石（Be3Al2Si2O8−Be）・コフィン石（U(SiO4)1-x(OH)4x−U）・霞石（NaAlAiO4−Al）・リシア輝石（LiAlSi2O6−Li）・リシア雲母（K(Li,Al)SiO4(OH)2−Li）などのごく限られた種類のものにしかすぎない。これは、珪酸塩鉱物の方が一般的に言って化学的に分解し難い、言いかえるとそれに必要なエネルギー量が大きいからに外ならない。
　ところで銅のような場合には、周知のように現在最も利用されている鉱物は黄銅鉱（CuFeS2）である。この鉱物は、種々の型式の銅鉱床を作って濃集していると同時に、各種の普通の岩石、特に火成岩類、中にもごく少量ながら広く分散して産出している。例えば、ごく普通の花崗岩類を顕微鏡下に観察すると、1−2平方センチメートル程度の面積の中に少数ではあるが黄銅鉱の微粒を見出す事は決してむずかしくはない。従って少なくとも原理的には、このような産状の黄銅鉱も在来の手法により選鉱して人為的に再濃集させる事は不可能ではない。しかし、経済的な点を考えに入れれば、無論現実的にはこれは無理である。ここで問題はもう一つ別な点にもある。それは、普通の岩石中の銅分は、このように銅の硫化鉱物の微粒として散点する分のほかに、この岩石を作る他種の鉱物、特に量の多い普通の造岩鉱物である珪酸塩鉱物、の結晶構造中にその微量成分として含まれている分もあるという事である。場合によっては量的には後者の分の方が多い事すらある。このように岩石・鉱床中での銅の存在状態（産状）には上の2種があって、利用という観点からするとこれらの間には大きな差がある。後者の場合には、選鉱という在来の手法ではその人為的濃集に著るしい制限があり、また母鉱物の分解には多大のエネルギーを必要とする。
　そこで仮に将来、それまで利用して来た銅の有用鉱床がまったく無くなってしまえば、次善の策として後者のような産状の銅分を回収・利用せざるを得ない事になるが、それには必要エネルギーその他の問題から実際上は極めて困難と考えざるを得ない。Skinnerはこの事を鉱物資源利用の場合の鉱物学的障壁と呼んだ（Skinner,B.J., 1976）。彼によれば、多くの非鉄金属（彼の言う地球化学的に乏しい金属）がその好例をなす。この関係を示したのが図�X-7である。

図�X-7　鉱物学的障壁（Skinner,B.J., 1976）
�T−地球化学的に乏しい金属。
�U−地球化学的に豊富な金属。
A−硫化物中に主成分として存在している場合。
B−他種鉱物中の結晶構造中に微量成分として存在している場合。
C−鉱物学的障壁。（別ウィンドウに拡大）

　（３）　通常の岩石の利用　　　これまでは、ある特定鉱物種または化学成分の鉱物資源はすべてそれらの鉱床を源として考える事を前提としていた。しかし実際には仮に金属鉱物資源を例としてすら、その源は鉱床だけに限られずに、普通の岩石を利用している場合が無いわけではない。例えば、金属アルミニウムを得る源は、世界のほとんどの国ではいずれもボーキサイト鉱床のみである。しかし先に述べたように、ソ連邦ではもう随分以前からその源の一つとして、霞石閃長岩という火成岩の1種の主要構成鉱物である霞石（NaAlSiO4、Al−19.0％）を利用している。また、アノーソサイトと呼ばれる火成岩の主要構成鉱物であるアノーサイト（斜長石の1種CaAl2Si2O8、Al−19.4％）を原料として金属アルミニウムを得ようとする試みが、例えばカナダなどで最近精力的に研究されている。これら霞石閃長岩とかアノーソサイトとかいう岩石は、巨大な岩体として世界各地にその存在が知られており、それらの世界全体での存在量も相当大きい。このほか、アルミニウム分に富むある種の粘土鉱物より成る礬土頁岩（写真�X-1,2）のような粘土質堆積岩も、将来のアルミニウム鉱物資源の一つとして名が挙げられている。実際に世界第2次対戦中、日本は中国東北地方の在る礬土頁岩から金属アルミニウムを作っていた。

写真�X-1　中国河南省焦作の“礬土頁岩”鉱床。
現在でもアルミニウム資源として稼行し、Alの他、Ga、Y、Nbなどを回収している。（別ウィンドウに拡大）

写真�X-2　鉱石にみられるウーライト組織を持つダイアスポア。
×80、単ニコル。（別ウィンドウに拡大）

　このように、ある種の金属鉱物資源としてすら、単にそれらの鉱床のみならず、普通の岩石の中にも、問題とする元素を主成分の一つとする鉱物に富むものの場合には、それらの鉱物資源として考え得るものも存在する。もちろんこれらは、ごく特別な例を除けば、現在のところ既知経済限界下鉱物資源量あるいは潜在鉱物資源量としてすら、まったく算え上げられていない場合が多い。しかし50-100年先の長い将来の事まで考えに入れるのならば、このような事も十分可能になる場合も増えて来ると思われるので、今からこの方面の基礎的研究や調査を積極的に手懸けておく事が必要だろう。
　非金属または工業用原料鉱物資源の場合には、上の関係は金属鉱物資源の場合よりもずっと一般的である。セメント原料としての石灰岩や耐火物・金属マグネシウム原料としてのドロマイトなどのごく普通の炭酸塩岩類の利用は、その良い例をなしている。石材・骨材・砂利･砂もまったくこの好例である。
　（４）　固体地球以外に在る鉱物資源　　　海洋水中に溶け込んでいる各種の成分は、もちろん鉱物ではないが、便宜上ここに取り上げておく事としよう。すでに古くから私たちは、太陽熱その他を利用して海洋水を蒸発・濃縮させ、最終的にはそこからの析出物を精製して塩化ナトリウム（食塩）などの海洋水中のある種の溶解成分を分離・利用してきた。現在いろいろな地質時代の地層の1種として見出されている岩塩層・加里塩層・石膏層などのいわゆる蒸発岩層は、大昔に同じ作用が自然界で大規模に行われて生じたものである。
　一方、その溶存量は0.01-0.00001ミリグラム／リットル程度と極めて低いが、実に多くの成分が海洋水中に溶け込んでいる。海洋水全体の量は極めて莫大（1.4×10¹⁸トン）なので、その中に含まれているこれら微量成分の総量もまた結構大きな値を持っている。例えば、銅･ウランなどはいずれもほぼ30億トン前後、金は600万トン弱と計算されている。これらの値は、大陸地殻上部でのそれらの総鉱床量にくらべても、注目に値する大きさである。これら海洋水中の有用成分の抽出・利用は、古くから人々の関心を集め、また実際に試みられた事もある。しかし何分にもそれらの濃度がごく低いので、これらを海洋水中から大量に得ようとすると、それに必要な海洋水量も大きく、またその操作に必要なエネルギー量も莫大となる。仮に技術的困難が解決されたとしても、余程経済条件に恵まれないと、その実行は容易な事ではない。現在日本でも、海洋水中からウランを回収・利用しようとの技術的研究が大分前から続けられて来ており、その一次濃集には成功しているが、最終的な利用は経済的にはまだ前途は遠い。
　陸地上の水、特に乾燥地帯での湖沼水･地下水に関しては、絶え間の無い蒸発作用の結果としてある種の成分に富むようになり、ありはその一部が析出・沈澱・堆積したりする事がしばしば起る。現世の塩湖水からの天然での析出または人為的な抽出などによる塩化ナトリウムやリチウム・硼素・カリウムなどの化合物の利用が各地で行われており、それらはいずれもすでに各種の鉱物資源量見積りの際の計算に組み入れられている。
　地球外の、例えば月その他の天体から必要な鉱物資源を得る事は、考える事は容易であり、またロマンもあるが、本当にどこにどんなものがどれだけあるかなどの点を具体的に調べる事や、また実際にその調査・採掘・運搬などの技術的・経済的可能性の将来をはっきり見透す事は、現在のところでは極めてむずかしい。現在またはここ30−50年程度の比較的近い将来に私たちに与えられるであろう諸条件の下では、まず第1に考えるべき事は、やはり手近かの大陸および海洋地殻内の鉱物資源を如何に上手に探査・開発･利用するかを考え、固体地球内の鉱物資源の種類と量とをさらに大きくする為の努力に勤める事ではないだろうか。
　（５）　再利用　　　資源の再利用が声高く叫ばれるようになったのはもう随分以前の事であった。なかでも屑鉄・屑鋼・屑銅などの再利用の歴史は到って古い。鉱物資源の有効利用という点では、これを補完するという事で再利用はもっと考えられて良い利点を十分持っている。それでは実際にはこれはどの程度にまで実行されているのだろうか。
　ここには、金属鉱物資源の再利用の現実について具体的な資料を表�X-13に示す。この度合いの大小は、種々の事情から金属の種類によって随分違っている。この表を一見すれば、例えば鉛･アンチモンのそれが他に比較して特に高い事がすぐ判るだろう。この表には載っていないが、鉄の場合もその再利用度は高い。これは、この種の金属の利用の仕方としてそれぞれの金属・合金を主体とした商品（例えば、鉄−鋼製品、鉛−蓄電池、アンチモン−活字、銅−銅製品など）の使用量が大きく、かつそれらの回収・選別もまた比較的に容易などの事情が関連している。しかも、これらの大部分は先進工業国自身の中で多く使われていて、言いかえれば自国内にあって、鉱石･精鉱などの海外からの輸入とは違って、それらの確保がより安定している便利さもある。

表�X-13　金属鉱物資源再利用度
	日本*1 1976	USA*2 1978	世界*2
			1978	2000予測
Cr		7.8	10.2	9.4
Ni		24.7	19.6	22.8
Co		5.1	5.6	11.1
W		13.2	14.4	15.1
Cu	9.0	21.1	19.8	25.0
Pb	25.7	45.6	33.4	41.7
Zn	11.2	6.3*3	5.6*3	6.6*3
Sn		25.0	10.7	10.8
Sb		58.6	50.9	47.5
Hg		7.3	6.8	8.8
Au		29.2	11.7	11.6
Ag		23.2	26.7	32.2
Al		8.5*3	6.0*3	9.5*3
*1：小佐野一男（1978）、*2：USBM（1981）、*3：非金属としての使用分をも含む

表�X-14　再利用によってもたらされるエネルギー節約量
	単位生産量当りに必要な エネルギー量（kcal/g）		エネルギー節約量
	一次金属	回収金属	（回収金属）／ （一次金属）比％	節約量（kcal/g）
Fe	3.7	1.4	37.8	2.3
Ti	108.5	45.1	41.6	63.4
Cu	11.6	1.5	12.9	10.1
Al	44.2	1.7	3.8	42.5
Mg	78.1	1.6	2.0	76.5
（Rome Club Rept. no.4, 1976）

　金属鉱物資源再利用の利点は、単に新たな鉱石生産量をより低く押えて、それら各種鉱物資源量の温存を計るという物質的利点だけではなくて、金属製錬に必要なエネルギー量を低めるという点でも大きく役立っている。いくつかの例を表�X-14に掲げておこう（なお前出表�W-8の再生の欄も参照）。これらによれば、回収金属の製錬に必要なエネルギー量は、一次金属のそれにくらべて鉄・チタンの40％前後から、アルミニウム･マグネシウムの僅か2-4％程度までにと、大きな節約の出来る事が示されている。これに鉱石の採掘・選鉱に必要なエネルギー量まで加えて考えれば、その節約量はさらに大きくなる。ただし、これらスクラップ類の市場からの回収・選別にどのくらいの手間・経費とエネルギーが必要なのかについては、残念ながら十分な資料は見当らない。
　いずれにせよ、鉱物資源の再利用には利点が多く、それらの有効利用が大きな役割りを荷っている事に間違いはない。今後ともその度合いは益々高まって行くだろう。しかし、鉱物資源の利用は他の一面で、利用された特定鉱物や特定成分が人類社会での消費を通じて自然界へ再び分散する過程をも含んでいる事を注意しておきたい。従って、この再利用にはある限りがあると考えなければならない。』