
統計の概要
統計の目的
産業連関表は、作成対象年次における我が国の経済構造を総体的に明らかにするとともに、経済波及効果分析や各種経済指標の基準改定を行うための基礎資料を提供することを目的に作成しています。
産業連関表とは
産業連関表は、1936年アメリカの経済学者W.W.レオンチェフ博士によって考案され、産業連関分析による経済予測等について、精度の高さと有用性が認められたことから、広く世界で使われるようになりました。彼は、その功績により1973年にノーベル経済学賞を受賞しました。
産業連関表は、一定期間(通常1年間)において、財・サービスが各産業部門間でどのように生産され、販売されたかについて、行列(マトリックス)の形で一覧表にとりまとめたものです。
ある1つの産業部門は、他の産業部門から原材料や燃料などを購入し、これを加工して別の財・サービスを生産し、さらにそれを別の産業部門に対して販売します。購入した産業部門は、それらを原材料等として、また、別の財・サービスを生産します。このような財・サービスの「購入→生産→販売」という連鎖的なつながりを表したのが産業連関表です。
産業連関表の仕組みを利用して、ある産業に新たな需要が発生した場合にどういう形で生産が波及していくのかを計算することができます。
現在、わが国では、10府省庁の共同作業による産業連関表(全国を対象としていることから「全国表」ともいう)を5年ごとに作成しているほか、地域産業連関表(日本を9つの地域に分割した各地域を対象に、経済産業省が5年ごとに作成)、都道府県・市産業連関表(都道府県・市を対象に、都道府県・市がおおむね5年ごとに作成)、延長産業連関表(全国表をベンチマークとして直近の産業構造を推計したもので、経済産業省が毎年作成)、国際産業連関表(国際間取引を詳細に記述したもので、経済産業省やアジア経済研究所が作成)、各種分析用産業連関表(分析目的に応じて各機関が作成)など、それぞれの目的に応じた多くの産業連関表が作成され、各界、各層に幅広く利用されています。
統計の沿革
わが国における産業連関表は、経済審議庁(現内閣府)と通商産業省(現経済産業省)がそれぞれ独自に試算表として作成した昭和26年を対象年次とするものが最初でした。
その後、関係府省において統一的な産業連関表を作成することが望ましいとする統計審議会の答申を受け、昭和30年表から、行政管理庁(現総務省)、経済企画庁(現内閣府)、農林省(現農林水産省)、通商産業省及び建設省(現国土交通省)の5省庁と集計・製表を担当する総理府統計局(現総務省統計局)を加えた6省庁による本格的な共同の作成作業が開始されました。その後、昭和35年表から運輸省(現国土交通省)及び労働省(現厚生労働省)が、昭和50年表から大蔵省(現財務省)、文部省(現文部科学省)、厚生省(現厚生労働省)及び郵政省(現総務省)の4省が作成作業に参加し、平成13年1月の省庁再編(環境省、金融庁が新たに参加)を経て、現在は10府省庁による共同作業により、産業連関表が作成されています。
参 考
産業連関表の構造と見方(PDF:420KB)
【見る→】
国民経済計算体系における産業連関表(PDF:296KB)
産業連関表の沿革と我が国における作成状況(PDF:261KB)
産業連関表の見直しの変遷(PDF:387KB)
産業連関表の仕組み
1 産業連関表の構造
産業連関表(取引基本表)を縦(列)方向に見ると、財・サービスの生産にあたって投入された原材料及び粗付加価値の構成が示されており、横(行)方向に見ると、生産された財・サービスの販売(産出)先の構成が示されています。
 |
2 産業連関表の見方
産業連関表は通常、取引基本表、投入係数表、逆行列係数表等からなっています。
以下に模式化した表で説明します。
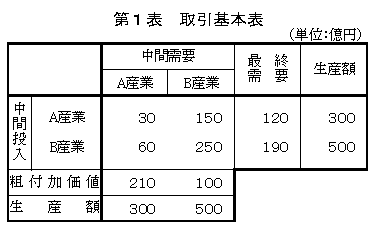
(1)取引基本表
A産業の構造は、以下のとおりとなっています。
列(縦)方向:
A産業(列)の生産額(300億円)は、原材料等としてA産業(行)から30億円、B産業(行)から60億円を購入(投入)したものと、粗付加価値は210億円からなっています。
行(横)方向:
A産業(行)で生産(300億円)されたものは、原材料等としてA産業(列)へ30億円、B産業(列)へ150億円販売し、最終需要には120億円販売しています。
なお、列方向と行方向の合計額は一致し、当該産業の生産額に等しくなっています。
 |
 |
 |