１ 産業連関表の構造と見方
(1) 産業連関表の構造
　国民経済を構成する各産業部門は、相互に網の目のように結び付き合いながら生産活動を行い、最終需要部門に対して必要な財・サービスの供給を行っている。
　ある一つの産業部門は、他の産業部門から原材料や燃料等を購入（投入）し、これを加工（労働・資本等を投入）して別の財・サービスを生産する。そして、その財・サービスをさらに別の産業部門における生産の原材料等として、あるいは家計部門等に最終需要として販売（産出）する。
　このような「購入−生産−販売」という関係が連鎖的につながり、最終的には各産業部門から家計、政府、輸出などの最終需要部門に対して必要な財・サービス（国内ではそれ以上加工されない）が供給されて、取引は終了する。
　食料関連産業を中心にこのような関連を見たのが第１図であり、各産業から原材料を購入し、完成財としての食料品を直接、又は飲食店などを通し間接的に家計、企業などの最終需要部門に対して供給している。

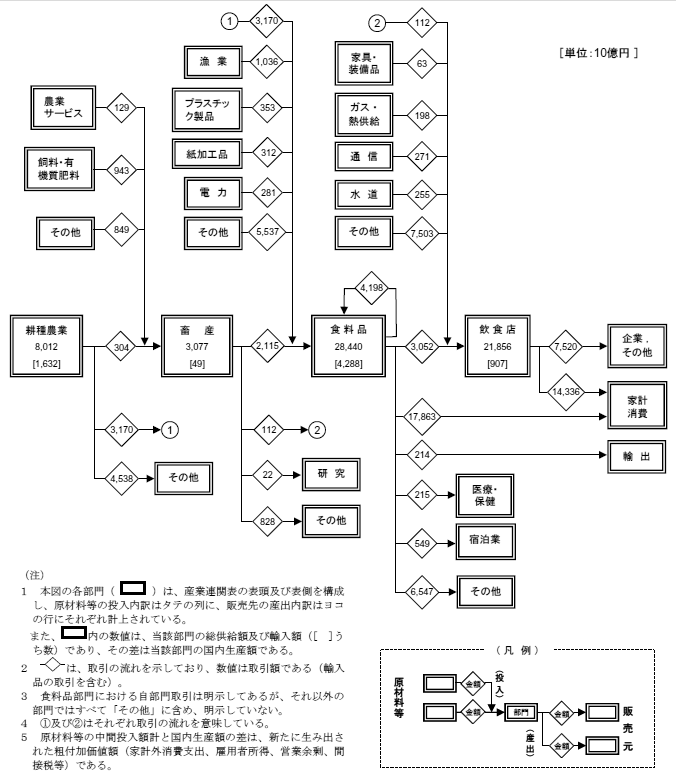
第１図 食料関連産業からみた他産業との関連

　産業連関表は、このようにして、財・サービスが最終需要部門に至るまでに、各産業部門間でどのような投入・産出という取引過程を経て、生産・販売されたものであるのかを、一定期間（通常１年間）にわたって記録し、その結果を第２図のような行列（マトリックス）の形で一覧表に取りまとめたものである。

ア 産業連関表の全体的な構成
　産業連関表の全体的な構成を第２図で見ると、表頭には、各財・サービスの買い手側の部門が掲げられ、大きく中間需要部門と最終需要部門から成っている。このうち、「中間需要部門」は、各財・サービスの生産部門であり、各部門は生産のために必要な原材料、燃料等のいわゆる中間財の購入（買い手）部門であり、これらを加工（労働、資本等を投入）して生産活動を行っている。
　また、「最終需要部門」は、具体的には消費、投資及び輸出であり、主として完成品としての消費財、資本財等の買い手である。
　一方、表側には、財・サービスの売り手側の部門が掲げられ、中間投入部門と粗付加価値部門から成っている。このうち、「中間投入部門」は、中間財としての各財・サービスの供給（売り手）部門であり、各部門は、当該部門の財・サービスを各需要部門に供給している。また、「粗付加価値部門」は、各財・サービスの生産のために必要な労働、資本などの要素費用その他である。
　産業連関表では、最終需要部門及び粗付加価値部門（すなわち、第２図の右及び下の突出した部分）を「外生部門」（exogenous sector）というのに対し、中間需要部門及び中間投入部門（同図中央の方形部分）を「内生部門」（endogenous sector）という。これは、外生部門の数値が他の部門とは関係なく独立的に決定されるのに対して、内生部門間の取引は、外生部門の大小によって受動的に決定されるというメカニズムの存在が前提にあるからである。
　なお、産業連関表のサイズ（部門数）は、例えば、行520 ×列407 や統合小分類190 部門というように、内生部門の数によって表す。

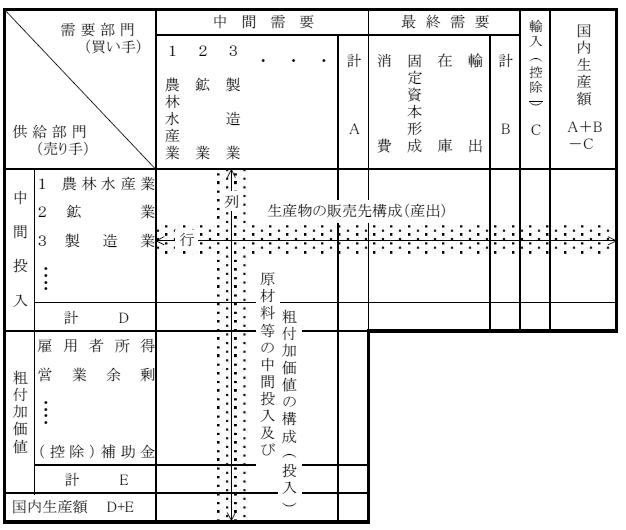
第２図 産業連関表の構造

イ 投入及び産出の構成
　産業連関表では、タテ方向の計数の並びを「列」 （column）という。列には、その部門の財・サービスの生産に当たって用いられた原材料、燃料、労働力などへの支払いの内訳（費用構成）が示されており、この支払いを産業連関表では、「投入」（input） と呼んでいる。
　一方、ヨコ方向の計数の並びを「行」（row） と呼ぶ。行には、その部門の財・サービスがどの需要部門でどれだけ用いられたのか、その販売先の内訳（販路構成）が示されており、この販売を「産出」（output）という。
　以上のように、産業連関表は、各産業部門における財・サービスの投入・産出の構成を示していることから、「投入産出表」（Input−Output Tables （略してＩ−Ｏ表））とも呼ばれている。

ウ 投入と産出とのバランス
　産業連関表では、列方向からみた投入額の計（国内生産額、第２図のＤ＋Ｅ）と行方向からみた産出額の計（国内生産額、同Ａ＋Ｂ−Ｃ）とは、定義を同じくするすべての部門について完全に一致しており、この点が大きな特徴となっている。
　タテ・ヨコの各部門の関係は、次のとおりである。
�@ 総供給＝国内生産額＋輸入額＝中間需要額計＋最終需要額計＝総需要
�A 国内生産額＝中間需要額計＋最終需要額計−輸入額＝中間投入額計＋粗付加価値額計
�B 中間投入額合計＝中間需要額合計
�C 粗付加価値額合計＝最終需要額合計−輸入額合計
　なお、�@及び�Aについては、各行・列の部門ごとに成立するが、�B及び�Cについては、産業計（部門の合計）についてのみ成立する。

(2) 産業連関表の見方
　産業連関表の全般的な構造をみてきたが、次に実際の計数に沿ってみていくこととしよう。

ア 簡単な数値事例による概念の整理
　産業連関表は、通常、取引基本表（狭義的にこれを単に産業連関表と呼ぶ場合もある。）、投入係数表、逆行列係数表等で構成されている。
(ｱ) 取引基本表
　取引基本表は、各産業間で取り引きされた財・サービスを金額で表示したものである。まず、第１表のような極めて簡単な事例の取引基本表を想定する。

第１表 取引基本表の事例

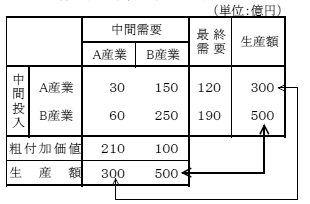　タテ（列）方向にＡ産業をみると、Ａ産業から30億円、Ｂ産業から60億円の原材料を購入し、210億円の粗付加価値を生み出すことで300億円の生産が行われたことを示す。また、Ａ産業をヨコ（行）にみると、生産額300億円のうち原材料としてＡ産業及びＢ産業へ各々30億円及び150億円、最終需要として120億円売られ（産出され）たことを示す。なお、タテの合計（投入額合計）とヨコの合計（産出額合計）は一致し、当該産業の生産額に等しい。本表では、Ａ産業の投入計及び産出計は300億円、Ｂ産業のそれは500億円となっている。
(ｲ) 投入係数表
　次に、本事例から投入係数を算出する。
　投入係数とは、取引基本表の中間需要の各列ごとに、原材料等の投入額を当該産業の生産額で除して得た係数であり、例えば第１表のＡ産業の列において投入係数を求めると、各投入額をＡ産業の生産額300億円で除したものとなる。言い換えれば、ある産業において１単位の生産を行う時に必要な原材料等の単位を示したものであり、これを使用することにより、産業間の連鎖を考察することも可能となる。これを産業別に一覧表にしたものが投入係数表であり、第１表の事例から算出される投入係数表は、第２表のとおりである。
(ｳ) 逆行列係数表
　逆行列係数とは、ある産業に対して１単位の最終需要があった場合（変化した場合）、各産業の生産が究極的にどれだけ必要となる（変化する）か、すなわち、直接・間接の究極的な生産波及の大きさを示す係数であり、数学上の逆行列を求める方法で算出することからこのように呼ばれる。

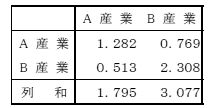
第２表 投入係数表の事例

　例えば、Ａ産業の最終需要が１単位発生した場合、直接的にはＡ産業の生産を１単位増加させなければならないが、そのためにはＡ産業の原材料投入も増加させる必要があり、Ａ産業が0.1 、Ｂ産業が0.2 生産増となる（第１次生産波及）。次に、Ａ産業0.1 及びＢ産業0.2 の生産増のために、投入される原材料生産の増加が要求（第２次生産波及）され、さらに、このような投入係数を介しての波及が第３図のように続いていく。この究極的な総和が逆行列係数に相当し、これを第３表のように産業別に一覧表にしたものが逆行列係数表である。
　また、逆行列係数は、特定部門の生産１単位をあげるのに、直接・間接に必要とされる諸産業部門の生産水準が、最終的にどのくらいになるかを算出した係数表ということもでき、この表の列和は、当該部門の需要が１単位発生したときの産業全体への波及合計に相当する。例えば本事例において、Ａ産業に最終需要が１単位発生した場合、全体で1.795 の生産波及効果を生じさせる。
　一方、生産誘発の観点からは、取引基本表における最終需要が生産額を誘発したとの見方もできる。第４図のとおり、Ａ産業の最終需要120億円によって、Ａ産業は直接、間接に154億円（＝120億円 ×1.282 ）、Ｂ産業は62億円（＝120億円 ×0.513 ）の生産が誘発され、またＢ産業の最終需要190億円によって、Ａ産業が146億円（＝190億円 ×0.769 ）、Ｂ産業が438億円（＝190億円 ×2.308 ）の生産が誘発される。
　この結果として、Ａ産業が300億円（＝154億円＋146億円）、Ｂ産業が500億円（＝62億円＋438億円）の生産をあげたのであり、第１表の生産額に一致する。
（以上、詳細は第５章を参照。）

第３表 逆行列計数表の事例

第３図 最終需要の発生と生産の波及

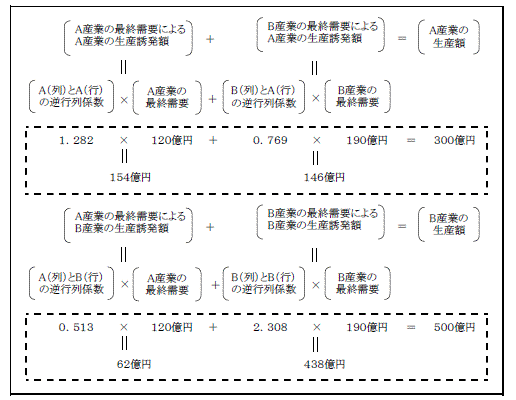
第４図 最終需要と生産誘発

イ 実際の産業連関表の見方
　それでは、実際の産業連関表を、平成17年産業連関表の13部門表（本編第１章の第１表及び第2章〔資料２〕の各表）に即してみていく。
　例えば、取引基本表（生産者価格評価表）の「03製造業」について、これをタテ（列）方向にみていくと、国内生産額が307兆709億円であり、その生産のために総額214兆4640億円の中間投入（内生部門計）が必要なこと、また、その内訳は、農林水産業から7兆7982億円、鉱業から12兆6381億円、製造業自身から132兆4270億円等々であったことが、各マス目の数字から読み取ることができる。さらに、その生産のためには雇用者所得46兆9015億円、営業余剰14兆2065億円などを必要とし、総額として92兆6069億円の粗付加価値が新たに生み出されたことが示されている。
　一方、ヨコ（行）方向に「03製造業」を取り上げてみると、まず、中間需要部門に対しては輸入品を含め総額198兆7509億円（内生部門計）が販売されている。いずれも中間財としての販売であり、その内訳は農林水産業に対して2兆5636億円、製造業自身に対して132兆4270億円、建設に対して17兆9675億円等々となっている。また、最終需要部門に対しては民間消費支出に56兆8106億円、国内総固定資本形成に34兆7007億円、輸出に56兆2489億円等々であり、最終需要全体で152兆3552億円となっている。
　中間需要と最終需要とを合わせた351兆1061億円が製造業に対する「総需要（需要合計）」である。これから輸入分の44兆352億円を控除した307兆709億円が製造業の国内生産分であり、列方向からみた国内生産額と一致する。

(3) 産業連関表の特徴
　産業連関表は、国民経済計算体系の中で財・サービスの流れ、すなわち実物的な「モノのフロー」面の実態を明らかにするものとして位置づけられている。
　１年間に生産された財・サービスのすべてが対象となり、内閣府が作成する国民経済計算では産業計のみ対象とする中間生産物についても、各産業部門別にその生産及び取引実態が詳細に記録されていることが大きな特色となっている。

ア 産業連関表の作成目的
　産業連関表（取引基本表）は、約行500×列400の部門について、行方向では中間需要も含めたマクロ需給バランス表、列方向では中間投入を含めた生産技術的マクロ経営（収支）バランス表となっている。また、内生部門（中間投入・需要部門）をみれば狭義の生産技術構造あるいは経済循環を、最終需要部門や粗付加価値部門をみれば部門別所得・支出勘定の情報を得ることができる。それに加えて、付帯表等を通して各セルごとの流通マージン、輸入量等の統計も提供するなど、一つの統計表でこれだけ多くのマクロ数量情報を供給しうるものは他になく、まさに、「経済構造（経済循環）に関する情報の宝庫」と称される所以ともなっている。
　これら極めて多量の統計値については、各種１次統計を収集、整理、加工等の後推計されることとなるが、実施の主体や、対象、方法、目的、時期等性格が異なる各種統計の相互の整合性をとりつつ推計が行われる。言い換えれば、各種１次統計が産業連関表としてまとめ上げられた時点で、これらが同じ性格を有することとなり、お互いに整合性のとれたものとなるわけであり、この意味で、産業連関表は「各種１次統計の規準化」という機能を有しているとも言えよう。この結果、１次統計時点では難しい部門（商品、産業）間の各種比較が、産業連関表を利用することで可能となる。
　なお、産業連関表の作成は、一定のルールに基づく産業連関表の部門分類に従って国民経済を一つの統計表にまとめ上げるという性格を有することから、その作成を通じて１次統計の不備・不足する分野が明らかにされ、当該分野における統計の整備・改善が進められることが期待される。このような意味で、２次統計である産業連関表が、その作成を通じて、我が国統計体系の整備に関し、フィードバック機能を有してきたとも言える。
　実世界の各種産業は、互いに取引関係を結びながら生産活動を営むという、複雑な相互依存関係の網の目を通じてつながっている。すなわち、ある部門に生まれた経済活動への刺激は、直接、間接、あるいは間接のまた間接といったルートを通じ、他の部門にも影響を及ぼしている。こうした波及効果（究極的な影響）がどの程度の大きさになるかを数量的に計測してくれるのが、経済の循環を一つの表としてまとめ上げた産業連関表であり、この種の分析を通常「産業連関分析」と称している。このように、経済波及等の計量的測定を可能とすることも、産業連関表のもつ大きな特徴である。

イ 国民経済計算との関係
　産業連関表の外生部門（粗付加価値部門と最終需要部門）は、第５図のようにバランスしており、このことを、粗付加価値部門と最終需要部門の「二面等価」という。

粗付加価値額合計 ＝ 最終需要額合計 − 輸入額合計
　　　　　　　(a) 　　　　　　　　　　　　　　　　(b)

第５図 外生部門のバランス関係

　このバランス式のうち(a)は国民経済計算の国内総生産（ＧＤＰ）（生産側）に、(b)は国内総生産（支出側）に「ほぼ」対応する。
　なお、対応関係が「ほぼ」であるのは、産業連関表では、国民経済計算と異なり、�@「家計外消費支出」（企業の交際費、福利厚生費等）を粗付加価値部門及び最終需要部門に含めていること、�A輸入品の投入・産出を「関税及び輸入品商品税」込みで記述することから、当該税が粗付加価値部門に含まれないこと、�B平成２年表以降は、在庫、投資も含め、原則としてすべての取引が消費税込みで記述されていることによる。
　このうち、もっとも大きな相違点は�@であり、平成17年表において、粗付加価値合計505兆8741億円から家計外消費支出合計の16兆8027億円を差し引いた489兆714億円が、国内総生産（ＧＤＰ）（生産側）に相当し（部門ごとにも同様で、例えば、製造業のＧＤＰ（生産側）＝92兆6069億円−4兆3133億円＝88兆2936億円）、他方、最終需要合計578兆3572億円から輸入合計72兆4831億円を控除し、家計外消費支出合計の16兆8027億円を差し引いた489兆714億円が、国内総生産（支出側）に相当しているといえる。両者は当然ながら一致（二面等価）する。

(4) 産業連関表の利用
　以上のように産業連関表は、これをそのまま読み取るだけでも、表の対象年次の産業構造や産業部門間の相互依存関係など国民経済の構造を総体的に把握・分析することができる。
　また、産業連関表では、タテとヨコの合計額が一致・バランスしているので、ある部門に変化が生じた場合はいったんはバランスを崩すこととなるが、究極的には、他部門への波及を通じて新しいバランス状態を生むこととなる。このように、経済活動相互間の全体的な関連をあらかじめ念頭に置かなければ解決できない問題に対して効果的な分析方法を提供するので、各種変化（例えば政策の変更）による経済効果のシミュレーションや、相互に整合性がとれた将来の経済構造の全体像を推定するといった予測分析等にも幅広く応用できる。
　主な利用方法を挙げると、次のとおりである。
〔経済構造の分析〕
　産業連関表には、各財・サービスの国内生産額、需要先別販売額（中間需要、消費、投資、輸出等）及び費用構成（中間投入、労働費用（雇用者所得）、減価償却費（資本減耗引当）等）が、各産業部門ごとに詳細に掲載されている。これらの計数により、例えば産業別投入構造や雇用者所得比率、各最終需要項目の商品構成や商品別の輸出入比率など、経済構造の特徴を読み取ることができる。
〔経済の予測〕
　産業連関表から投入係数、逆行列係数などの各種係数が計算されるが、これらの係数により、投資や輸出の増加などの最終需要の変化が各財・サービスの生産や輸入にどのような影響を及ぼすかを、計数的に明らかにすることができる。これは、経済に関する各種計画や見通しの作成の際に広く用いられる方法である。
〔経済政策の効果測定〕
　経済の予測と同様に、最終需要と各財・サービスの生産水準等との関係を利用して、特定の経済政策が各産業部門にどのような影響をもたらすかを分析することができる。財政支出や減税実施の波及効果の測定、公共投資の経済効果の測定などがそれである。
〔他の経済統計の基準値〕
　我が国の産業連関表は、５年ごとに、あらゆる統計資料を用いて精密に作成されており、その結果は各種の経済統計において基準値として利用されている。
　例えば、内閣府の「国民経済計算」の推計においては、５年ごとの基準改定に当たり、産業連関表が重要な基礎統計として活用されている。また、産業連関表の部門別付加価値額や中間需要額を利用して、「第３次産業活動指数」（経済産業省）や「企業向けサービス価格指数」（日本銀行）などの作成のためのウェイトが計算されている。さらに、毎年作成されている産業連関表の延長表（経済産業省）も、５年ごとの産業連関表を基にして、これにその後の計数の変化を加味して推計されているものである。